算法理解|从头开始理解梯度提升算法
简化复杂的算法
动机
尽管大多数的Kaggle竞赛的获胜者使用了多个模型的集成,这些集成的模型中,有一个必定是各种变体的梯度提升算法。举个例子,Kaggle竞赛: Safe Driver Prediction:https://www.kaggle.com/c/porto-seguro-safe-driver-prediction/discussion/44629#250927,Michael Jahrer的方案,使用了表示学习,使用了6个模型的综合。1个LightGBM和5个神经网络。尽管他的成功归功他使用了结构化的数据进行了半监督学习,梯度提升算法也实现了非常重要的部分。
尽管GBM使用的非常广泛,许多使用者仍然把这个东西当做一个黑盒子算法,只是使用预编译好的库跑一跑。写这篇文章的目的是简化复杂的算法,帮助读者可以直观的理解算法。我会解释原汁原味的梯度提升算法,然后分享一些变种的链接。我基于fast.ai的库做了一个决策树的代码,然后构建了一个自己的简单的基础的梯度提升模型。
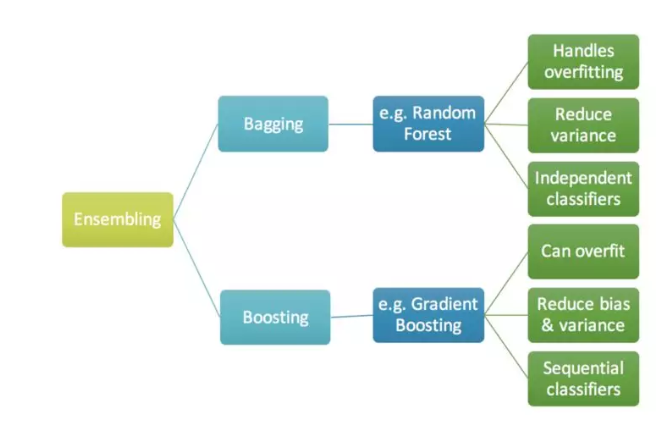
Ensemble, Bagging, Boosting的简单描述
当我们使用一个机器学习技术来预测目标变量的时候,造成实际值和预测值之间的差别的原因有噪声,方差和偏差。集成方法能够帮助减少这些因素(除了噪声,不可约误差)。
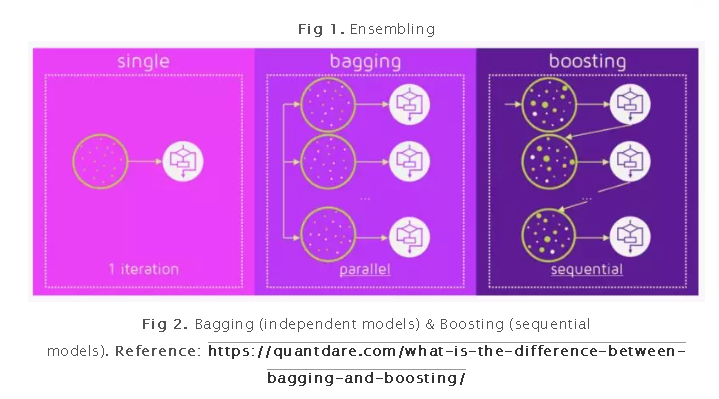
Ensemble是几个预测器在一起(比如求平均),给出一个最终的结果。使用ensemble的原因是许多不同的预测器预测同一个目标会比单个预测器的效果要好。Ensemble技术又可以分成Bagging和Boosting。
Bagging是一个简单的ensemble的技术,我们构建许多独立的预测器/模型/学习器,通过模型平均的方式来组合使用。(如权值的平均,投票或者归一化平均)
我们为每个模型使用随机抽样,所以每个模型都不太一样。每个模型的输入使用有放回的抽样,所以模型的训练样本各不相同。因为这个技术使用了许多个不相关的学习器来进行最终的预测,它通过减少方差来减小误差。bagging的一个例子是随机森林模型。
Boosting 在对模型进行ensemble的时候,不是独立的,而是串行的。
这个技术使用了这样的逻辑,后面的预测器学习的是前面的预测器的误差。因此,观测数据出现在后面模型中的概率是不一样的,误差越大,出现的概率越高。(所以观测数据不是基于随机又放回抽样bootstrap的方式,而是基于误差)。预测器可以从决策树,回归器,分类器中选取。因为新的预测器是从前面的预测器的误差中学习的,接近实际的预测只需要更少的时间和迭代次数。但是我们不得不选择严格的停止策略,否则可能会出现过拟合。梯度提升算法就是提升算法的一个例子。
梯度提升算法
梯度提升是一个机器学习技术,用来做回归和分类的问题,通过组合弱预测模型如决策树,来得到一个强预测模型。(维基百科定义)
监督学习算法的目标是定义一个损失函数,然后最小化它。我们来看看,数学上梯度提升算法是怎么工作的。比如我们使用均方误差(MSE)作为损失函数:

所以,我们基本上是在更新预测,让残差的和接近于0(或者最小),这样预测的值就和实际的值足够的接近了。
梯度提升背后的直觉
梯度提升背后的逻辑很简单,(可以很直观的理解,不用数据公式)。我希望读这篇文章的人能够熟悉一下简单的线性回归模型。
线性回归模型的一个基本的假设是残差是0,也就是说,参数应该在0的周围分散。

现在,把这些残差作为误差提交到我们的预测模型中。尽管,基于树的模型(将决策树作为梯度提升的基础模型)不是基于这个假设,但是如果我们对这个假设进行逻辑思考,我们也许能提出,如果我们能发现在0的周围的残差一些模式,我们可以利用这个模式来拟合模型。
所以,梯度提升背后的直觉就是重复的利用残差中的模式利用弱预测器来加强模型,让模型变得更好。一旦我们到了一个阶段,残差不具有任何的模式,无法进行建模,我们就可以停止了(否则会导致过拟合)。从算法的角度讲,我们在最小化损失函数,直到测试损失达到最小。
总结一下:
我们首先使用一个简单的模型对数据进行建模,分析数据的误差。
这些误差表示数据点使用简单的模型很难进行拟合。
然后对于接下来的模型,我们特别的专注于将那些难于拟合的数据,把这些数据预测正确。
最后,我们将所有的预测器组合起来,对于每个预测器给定一个权重。
拟合梯度提升模型的步骤
我们来模拟一些数据,如下面的散点图所示,一个输入,一个输出。
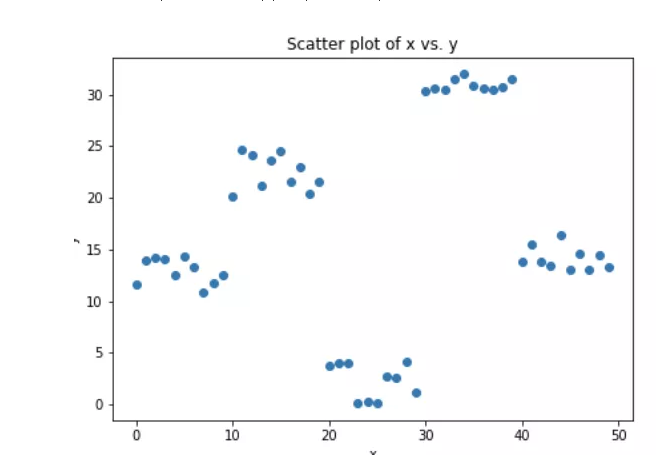
上面的数据是通过下面的python代码生成的。
x = np.arange(0,50)
x = pd.DataFrame({'x':x})
# just random uniform distributions in differnt range
y1 = np.random.uniform(10,15,10)
y2 = np.random.uniform(20,25,10)
y3 = np.random.uniform(0,5,10)
y4 = np.random.uniform(30,32,10)
y5 = np.random.uniform(13,17,10)
y = np.concatenate((y1,y2,y3,y4,y5))
y = y[:,None]1. 拟合一个简单的线性回归模型或者决策树模型(在我的代码中选择了决策树)[x作为输入,y作为输出]
xi = x # initialization of input
yi = y # initialization of target
# x,y --> use where no need to change original y
ei = 0 # initialization of error
n = len(yi) # number of rows
predf = 0 # initial prediction 0
for i in range(30): # loop will make 30 trees (n_estimators).
tree = DecisionTree(xi,yi) # DecisionTree scratch code can be found in shared github/kaggle link.
# It just create a single decision tree with provided min. sample leaf
tree.find_better_split(0) # For selected input variable, this splits (<n and >n) data so that std. deviation of
# target variable in both splits is minimum as compared to all other splits
r = np.where(xi == tree.split)[0][0] # finds index where this best split occurs
left_idx = np.where(xi <= tree.split)[0] # index lhs of split
right_idx = np.where(xi > tree.split)[0] # index rhs of split2.计算误差,实际的目标值,最小化预测目标值 [e1= y - y_predicted1 ]
3.把误差作为目标值,拟合新的模型,使用同样的输入数据[叫做e1_predicted]
4. 将预测的误差加到之前的预测之中[y_predicted2 = y_predicted1 + e1_predicted]
5. 在剩下的残差上拟合另一个模型, [e2 = y - y_predicted2],重复第2到第5步,直到开始过拟合,或者残差的和开始不怎么变换。过拟合可以通过验证数据上的准确率来发现。
# predictions by ith decisision tree
predi = np.zeros(n)
np.put(predi, left_idx, np.repeat(np.mean(yi[left_idx]), r)) # replace left side mean y
np.put(predi, right_idx, np.repeat(np.mean(yi[right_idx]), n-r)) # right side mean y
predi = predi[:,None] # make long vector (nx1) in compatible with y
predf = predf + predi # final prediction will be previous prediction value + new prediction of residual
ei = y - predf # needed originl y here as residual always from original y
yi = ei # update yi as residual to reloop为了帮助理解划线部分的概念,这里有个链接,有完整的梯度提升模型的实现 [[Link: Gradient Boosting from scratch]](https://www.kaggle.com/grroverpr/gradient-boosting-simplified/)。
梯度提升树的可视化工作
蓝色的点(左边)是输入(x),红色的线(左边)是输出(y)显示了决策树的预测值,绿色的点(右边)显示了第i次迭代的残差vs.输入(x),迭代表示拟合梯度提升树的了序列的顺序。
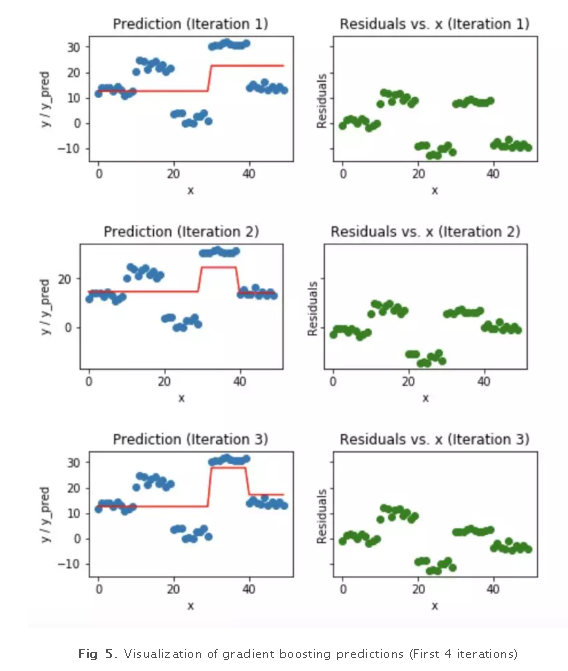
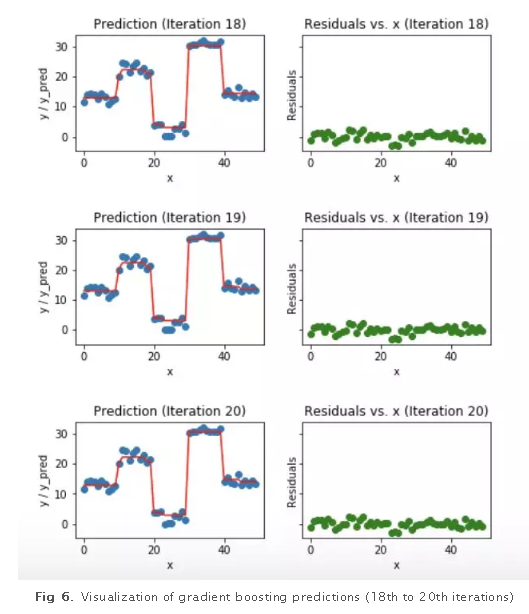
我们发现过了20个迭代,残差变成了0附近的随机分布(我不会说是随机正态分布),我们的预测也非常接近于实际值。这时可以停止训练模型了,否则要开始过拟合了。
我们来看看,50个迭代之后的样子:
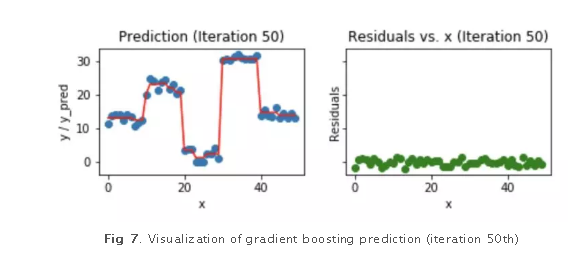
我们发现,即使是50个迭代之后,残差vs. x的图和我们看到的20个迭代的图也没太大区别。但是模型正在变的越来越复杂,预测结果在训练数据上出现了过拟合。所以,最好是在20个迭代的时候就停止。
用来画图的python代码。
# plotting after prediction
xa = np.array(x.x) # column name of x is x
order = np.argsort(xa)
xs = np.array(xa)[order]
ys = np.array(predf)[order]
#epreds = np.array(epred[:,None])[order]
f, (ax1, ax2) = plt.subplots(1, 2, sharey=True, figsize = (13,2.5))
ax1.plot(x,y, 'o')
ax1.plot(xs, ys, 'r')
ax1.set_title(f'Prediction (Iteration {i+1})')
ax1.set_xlabel('x')
ax1.set_ylabel('y / y_pred')
ax2.plot(x, ei, 'go')
ax2.set_title(f'Residuals vs. x (Iteration {i+1})')
ax2.set_xlabel('x')
ax2.set_ylabel('Residuals')我希望这个博客可以帮助你对梯度提升算法的工作有一个基本的直觉。为了理解梯度提升回归算法的细节,我强烈建议你读一读下面这些文章。
更多有用的资源
我的github仓库和kaggle的kernel的链接,从头开始GBM
https://www.kaggle.com/grroverpr/gradient-boosting-simplified/https://nbviewer.jupyter.org/github/groverpr/Machine-Learning/blob/master/notebooks/01_Gradient_Boosting_Scratch.ipynb
一个直观和细致的梯度提升算法的解释
http://explained.ai/gradient-boosting/index.html
Fast.ai的github仓库链接,从头开始做决策树
https://github.com/fastai/fastai
Alexander Ihler的视频,这视频帮我理解了很多。
https://youtu.be/sRktKszFmSk
最常用的GBM算法
XGBoost || Lightgbm || Catboost || sklearn.ensemble.GradientBoostingClassifier






评论专区