二维码

新兴竞争币代表：超级现金 - 数据结构 - 机器学习

1446 人阅读 | 时间：2021年01月15日 01:06
新兴竞争币代表：超级现金 - 数据结构 - 机器学习 #daohang ul li t,.reed .riqi,a.shangg,a.xiatt,a.shangg:hover,a.xiatt:hover,a.shang,a.xiat,a.shang:hover,a.xiat:hover,.reed-pinglun-anniu,span.now-page,#daohangs-around,#caidan-tubiao,#daohangs,#daohangs li,#btnPost{background-color:#D10B04;} .dinglanyou1 h3{border-bottom:3px solid #D10B04;} #dibuer{border-top:2px solid #D10B04;}.cebianlan .rongqi h3{border-bottom:1px solid #D10B04;} #edtSearch{border:1px solid #D10B04;} #daohang .zuo ul li{border-right:1px solid #;} #daohang ul li t a{border-top:1px solid #;border-right:1px solid #D10B04;} #daohang ul li t a:hover{border-right:1px solid #;} #daohang .you ul li a:hover,#daohang .zuo ul li a:hover,.reed-pinglun-anniu:hover{background-color:#;} a:hover,.reed h6 a:hover,#dibuer a:hover,.reed .riqiding,.cebianlan .rongqi li a:hover,#pinglun-liebiao ul.fubens li.depth-1 dl dd span.shu a,#pinglun-liebiao ul.fubens li.depth-1 dl dd span.huifuliuyan a:hover,.reed-biaoti h6 span{color:#D10B04;} .reed .kan a{color:#0A0AF5;}.reed .kan a:hover{color:#D10101;} @media screen and (max-width:1492px){a.shang,a.xiat{background:none;} a.xiat:hover,a.shang:hover{background-color:#f9f9f9;background-image:none;text-decoration:none;}} var _hmt = _hmt || [];(function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?b19db5ba3b437a9e8698d2bc8fc64334"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s);})(); var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?b19db5ba3b437a9e8698d2bc8fc64334"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })(); var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?2d748c9763cfc72fb7d1ccab29f0770d"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })(); var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?f6d451f3f1be23f3abf240c64c469c1b"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })();

当前位置：首页 » 区块链精品文章 » 正文

(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646201", container: s }); })();
(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646162", container: s }); })();

新兴竞争币代表：超级现金

1039 人参与  2018年08月28日 13:42  分类 : 区块链精品文章  评论

比特币和以太坊为我们打开了新世界的大门，向我们证明了区块链技术的价值和内在的潜力。随着比特币价值的水涨船高，各种数字货币层出不穷。

从2015年开始，一些非常有潜力的但是并不基于区块的分布式账本系统底层技术也逐渐进入我们的视野，如DAG——有向无环图。

然而，一个最大的问题是：这几种基于完全不同系统的货币目前除了在中心化的交易所进行兑换外，并不能在这两种完全不同体系的分布式系统中自由流通。

超级现金（Hcash）就是这样一种可以实现各区块价值互联的载体。它可以连通基于区块的分布式账本和不基于区块的分布式去中心化账本系统，让所有这些去中心化的分布式账本之间的信息与价值自由流通。

超级现金：打破数字货币之间的隔阂

首先，我们给超级现金下一个定义：

超级现金是一种新型的数字加密货币，它可以成为连接区块链和DAG这两种不同技术的分布式记账系统的桥梁。

通俗地讲，比特币和以太坊为我们打开了新世界的大门，向我们证明了区块链技术的价值和内在的潜力。随着比特币价值的水涨船高，各种数字货币层出不穷。

从2015年开始，一些非常有潜力的但是并不基于区块的分布式账本系统底层技术也逐渐进入我们的视野，如DAG——有向无环图。

毋庸置疑，在未来去中心化的数字世界里，比特币或者以太币或许会成为区块链分布式账簿的基础货币，而基于DAG技术基础的货币或许会是IOTA（或Byteball）以及其他新兴数字货币。

然而，一个最大的问题是：这种基于完全不同系统的货币之前除了在中心化的交易所进行兑换外，并不能在这两种完全不同体系的分布式系统中自由流通。

据CoinMarketCap的数据统计，截至2017年6月13日，全球数字资产总市值已经超过了1100亿美元，其 中，市值在1亿美元以上的数字货币有40种。另据Cryptocoincharts显示，全球数字资产的种类已经达到4321种。随着全球数字资产数量和 种类不断增多，跨区块间以及跨系统间的流通，已经势在必行。

如何实现链条之间的互相连接？

超级现金就是这样一种可以实现各区块价值互联的载体。它可以连通基于区块的分布式账本和不基于区块的分布式去中心化账本系统，让所有这些去中心化的分布式账本之间的信息与价值自由流通。

为了方便大家理解，我们可以给“超级现金”一个更全面的定义：本质上，超级现金是区块链和DAG系统的双重侧链。超级现金将建立一个新的底层技术平台以链接各种不同的区块链技术，从而让基于信任的价值在不同的区块链系统中自由流通。[1]

DAG

超级现金是基于区块链和DAG系统的双重侧链。这里我们简单介绍一下什么是DAG。

DAG，英文全称是directed acyclic graph（有向无环图），就是用不同区块“图”式结构打破传统链式结构，如图2所示。

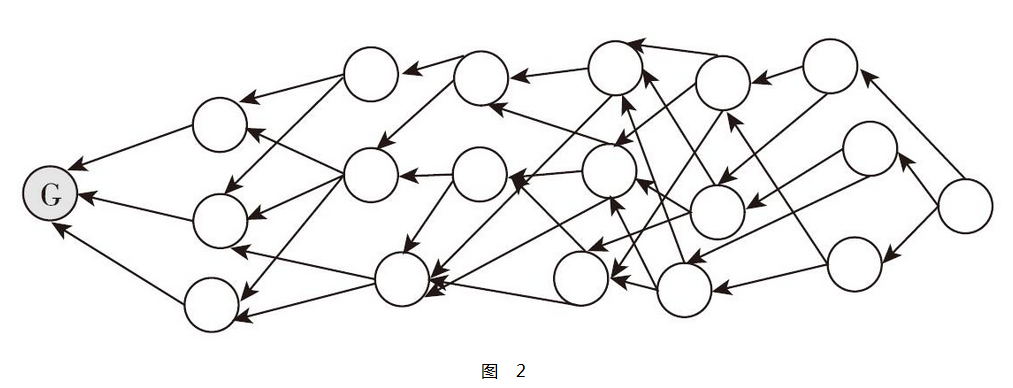
新兴竞争币代表：超级现金 - 数据结构 - 机器学习

DAG是区块链的扩容方案。

为什么要扩容呢？答案是显而易见的，10分钟1MB太慢了。

以比特币为例，比特币区块速度是每10分钟1MB，一个区块1MB，一般来说可容1440笔交易。也就是说，当我们进行转账时，每分钟只能通过144笔交易。这种时候，焦急的用户只能通过提高手续费来让自己的交易尽快被矿工打包。

如果简单地提高区块容量，例如一个区块加到100MB，由于网速的限制会导致很多节点还没有收到或者下载完新区块，下一 个区块就挖出来了，结果就是全网的不一致性提高（大家不在同一条链上挖矿），在同一条链上挖矿的算力降低，导致可靠性降低。更浅显一点的理解：传统区块链 采取的是最长链，由于网络的延迟，那么很可能实际上网络里最长的链上，只有一半的算力，另外一半的算力还没来得及去挖的时候，这条链已经多了一个新区块 了。从攻击者的角度讲——原来你要和全网所有其他算力竞争，现在，只要打赢一半算力就能进行51%攻击了。

DAG的解决方案是，将最长链共识改成最重链共识。每个挖出来的区块，不仅仅连在之前的一个区块上，而是连在所有区块 上。随着时间递增，所有交易的区块链相互连接，形成图状结构，如若要更改数据，那就不仅仅是几个区块的问题了，而是整个区块图的数据更改。DAG这个模式 相比来说，复杂度更高，更难以被更改。

这种情况下，如果有攻击者想以打赢一半的算力进行攻击，那么诚实节点会看到攻击者的链和另外一个DAG虽然一样长，但是 攻击者的链上每层都只有一个块，而这个DAG上每层有两个块，于是这个DAG更重，按照规则，不选链而选DAG。DAG的好处就是即便增加区块大小或者区 块频率造成网络里产生大量分叉，攻击者还是需要51%的算力才能进行攻击。

DAG（有向无环图）是不同于区块链的一种分布式账本技术，是数字资产界的一次较大的创新。DAG技术给高并发的交易提供了解决方案，把区块链二维的模式提升到三维。

[1] 来自于官方发布的《超级现金白皮书》。


来源：我是码农，转载请保留出处和链接！

本文链接：http://www.54manong.com/?id=134

(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646208", container: s }); })();
(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646147", container: s }); })();
window._bd_share_config={"common":{"bdSnsKey":{},"bdText":"","bdMini":"2","bdPic":"","bdStyle":"0","bdSize":"16"},"share":{},"image":{"viewList":["qzone","tsina","tqq","renren","weixin"],"viewText":"分享到：","viewSize":"16"},"selectShare":{"bdContainerClass":null,"bdSelectMiniList":["qzone","tsina","tqq","renren","weixin"]}};with(document)0[(getElementsByTagName('head')[0]||body).appendChild(createElement('script')).src='http://bdimg.share.baidu.com/static/api/js/share.js?v=89860593.js?cdnversion='+~(-new Date()/36e5)];
区块链是什么  

微信号：qq444848023    QQ号：444848023

加入【我是码农】QQ群：864689844（加群验证：我是码农）

<< 上一篇 下一篇 >>
(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646186", container: s }); })();
(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646175", container: s }); })();
搜索

网站分类

标签列表

最近发表

    (function(){ var bp = document.createElement('script'); var curProtocol = window.location.protocol.split(':')[0]; if (curProtocol === 'https'){ bp.src = 'https://zz.bdstatic.com/linksubmit/push.js'; } else{ bp.src = 'http://push.zhanzhang.baidu.com/push.js'; } var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(bp, s); })();

全站首页 | 数据结构 | 区块链| 大数据 | 机器学习 | 物联网和云计算 | 面试笔试

var cnzz_protocol = (("https:" == document.location.protocol) ? "https://" : "http://");document.write(unescape("%3Cspan id='cnzz_stat_icon_1276413723'%3E%3C/span%3E%3Cscript src='" + cnzz_protocol + "s23.cnzz.com/z_stat.php%3Fid%3D1276413723%26show%3Dpic1' type='text/javascript'%3E%3C/script%3E"));本站资源大部分来自互联网，版权归原作者所有！

jQuery(document).ready(function($){ /* prepend menu icon */ $('#daohangs-around').prepend('
'); /* toggle nav */ $("#caidan-tubiao").on("click", function(){ $("#daohangs").slideToggle(); $(this).toggleClass("active"); }); });

©著作权归作者所有：来自ZhiKuGroup博客作者没文化的原创作品，如需转载，请注明出处，否则将追究法律责任 来源：ZhiKuGroup博客，欢迎分享。

评论专区
  • 昵 称必填
  • 邮 箱选填
  • 网 址选填
  • 验证码
◎已有 0 人评论
相关文章
搜索
作者介绍
superadmin

superadmin

30天热门
热评文章
最近发表
标签列表

©2012-2022 Think tank 鄂ICP备19030179号-1 | 使用Chrome浏览本站最佳 | 声明：本站的文章和资源来自互联网或者站长的原创，按照 CC BY -NC -SA 3.0 CN协议发布和共享，转载或引用本站文章应遵循相同协议。 如果有侵犯版权的资源请尽快联系站长，我们会在24h内删除有争议的资源； 本站所有收费以及免费的信息和数据仅供参考，不构成投资建议，本网站不承担由此导致的任何责任。
登陆

Powered By Z-BlogPHP

本站会员尊享VIP特权，现在就加入我们吧！登录注册×
»
会员登录
新用户注册
×
会员注册
已有账号登录
×