二维码

树与二叉树的表示和基本操作 - 数据结构 - 机器学习

1416 人阅读 | 时间：2021年01月15日 01:07
树与二叉树的表示和基本操作 - 数据结构 - 机器学习 #daohang ul li t,.reed .riqi,a.shangg,a.xiatt,a.shangg:hover,a.xiatt:hover,a.shang,a.xiat,a.shang:hover,a.xiat:hover,.reed-pinglun-anniu,span.now-page,#daohangs-around,#caidan-tubiao,#daohangs,#daohangs li,#btnPost{background-color:#D10B04;} .dinglanyou1 h3{border-bottom:3px solid #D10B04;} #dibuer{border-top:2px solid #D10B04;}.cebianlan .rongqi h3{border-bottom:1px solid #D10B04;} #edtSearch{border:1px solid #D10B04;} #daohang .zuo ul li{border-right:1px solid #;} #daohang ul li t a{border-top:1px solid #;border-right:1px solid #D10B04;} #daohang ul li t a:hover{border-right:1px solid #;} #daohang .you ul li a:hover,#daohang .zuo ul li a:hover,.reed-pinglun-anniu:hover{background-color:#;} a:hover,.reed h6 a:hover,#dibuer a:hover,.reed .riqiding,.cebianlan .rongqi li a:hover,#pinglun-liebiao ul.fubens li.depth-1 dl dd span.shu a,#pinglun-liebiao ul.fubens li.depth-1 dl dd span.huifuliuyan a:hover,.reed-biaoti h6 span{color:#D10B04;} .reed .kan a{color:#0A0AF5;}.reed .kan a:hover{color:#D10101;} @media screen and (max-width:1492px){a.shang,a.xiat{background:none;} a.xiat:hover,a.shang:hover{background-color:#f9f9f9;background-image:none;text-decoration:none;}} var _hmt = _hmt || [];(function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?b19db5ba3b437a9e8698d2bc8fc64334"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s);})(); var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?b19db5ba3b437a9e8698d2bc8fc64334"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })(); var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?2d748c9763cfc72fb7d1ccab29f0770d"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })(); var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?f6d451f3f1be23f3abf240c64c469c1b"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })();

当前位置：首页 » 数据结构精品文章 » 正文

(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646201", container: s }); })();
(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646162", container: s }); })();

树与二叉树的表示和基本操作

1723 人参与  2018年09月03日 22:40  分类 : 数据结构精品文章  评论

1、树的表示方法有哪几种？

树的表示方法有以下四种，各用于不同的目的

1）直观表示法

以倒着的分支树的形式表示。是数据结构中最常用的树的描述方法。

其特点就是对树的逻辑结构的描述非常直观。

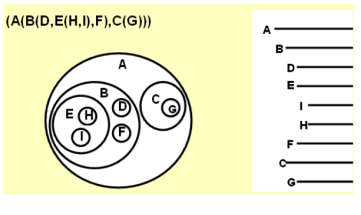
2）嵌套集合表示法

将根结点视为一个集合，其子树构成集合中若干个互不相交的子集，如此嵌套下去，即构成一棵树的嵌套集合表示。

3）凹入表示法  主要用于树的屏幕和打印输出。

4）广义表表示法  将根作为由子树森林组成的表的名字写在表的左边，这样依次将树表示出米。

2、树的基本操作

InitTree(&T)初始化一棵空树T。

DestroyTree(&T)树T存在，现销毁树T。

CreateTree(&T，definition)按definiti给出树T的定义构造树T。

ClearTree(&T)树T存在，现将树T清为空。

TreeEmpty(T)若T为空树返回TRUE，否则FALSE。

TreeDepth(T)返回树T的深度。

Value(T，cur-e)cur-e是树T中某个结点，返回cur-e的值。

Assian(T，cur-e，value)给树中结点cur-e赋值为value。

Root(x)求结点x所在树的根结点。   Parent(T，cur-e)求树T中结点cur-e的双亲。若cur-e是T的非根结点，则返回它的双亲，否则函数值为“空”。

LeftChild(T，cur-e)若cur-e是T的非叶子结点，则返回它的最左孩子，否则返回“空”。

RightSibling(T，cur-e)若cur-e有右兄弟，则返回它的右兄弟，否则函数值为“空”。

InsertChild(&T，&p，i，c)把以c为根结点的树，插入到树T中作为结点p的第i棵子树。

DeleteChild(&T，&p,i)删除T中p所指结点的第i棵子树。

p指向T中某个结点，1≤i≤p指结点的度。

TraverseTree(T，Visit())visit是对树的遍历操作。按某种次序对T的每个结点调用visit()一次且至多一次。一旦visit()失败，则操作失败。

树与二叉树的表示和基本操作 - 数据结构 - 机器学习 

3、树的双亲表示法

由树的定义，树中的每个结点都有唯一的一个双亲结点，根据这一特性，可用一组连续的存储空间(一维数组)存储树中的各个结点，数组中的一个元素表示树中的一个结点，数组元素为结构体类型，其中包括结点本身的信息以及结点的双亲结点在数组中的序号。

树的这种存储方法称为双亲表示法。

#define MAXNODE<树中结点的最大个数>

typedef struct {

elemtype data；

int  parent；

}NodeType；

NodeType t{MAXNODE}；

4、二叉树的定义

1）定义：每个结点至多有两棵子树的有序树。

结点的度≤2(每个结点至多两棵子树)+左右有别(有序)。

2）二叉树的ADT定义

数据对象D

数据关系R

其余比照树的定义。

D是具有相同特性的数据元素的集合。

若D=φ，称BlnaryTree为空二叉树；若D≠φ，则R={H}是如下二元关系

1、在D中存在唯一的称为根的数据元素root，它在关系H下无前驱；

2、在D-{root}≠φ，则存在D-{root}={D1，Dr，)，且D1∩Dr=φ；

3、若D1≠φ，则D1中存在唯一元素x1，(root，x1)∈H，且存在D1上的关系H1H；若Dr≠φ，则Dr中存在唯一元素xr，(root，xr)∈H，且存在Dr上的关系HrH；

H={(root，x1)，(root，xr)，H1，Hr)；

4、(D1，{H1})是一棵符合本定义的二叉树，称为根的左子树，(Dr，{Hr})是一棵符合本定义的二叉树，称为根的右子树。

5、二叉树的基本操作

与树相仿，但分左右，操作位置更为明确

InitBiTree(&T)  置空  构造空二叉树T。

DestroyBiTree(&T)  “收回”  销毁二叉树T。

CreateBiTree(&T，definition)  新建  按definiti定义的二叉树构造二叉树T。

ClearBiTree(&T)  清空  将二叉树T清为空。

BiTreeEmpty(T)  判空  若T为守返回TRUE，否则返回FALSE。

BiTreeDepth(T)：  求深度  返回T的深度。

Root(T)  求根  返回T的根。

Value(T，e)  求值  e是T中某个结点。返回e的值。

Assign(T，&e，value)  赋值  T中结点e赋值为value。

Parent(T，cur-e)  求父结点  若e是T的非根结点，则返回它的双亲，否则函数值为“空”。

LeftChild (T，e)  求e的左孩子。若e无左孩子，则返回“空”。

RightChild (T，cur-e)  求cur-e的右孩子。若e无右孩子，则返回“空”。

LeftSibling (T，e)  求e的左兄弟。若e是T的左孩子或无左兄弟，则返回“空”。

RightSiblinq(T，e)  求e的右兄弟。若e是T的右孩子或无右兄弟，则返回“空”。

InsertChild(T，p，LR，c)  插入字数  p指向T中某个结点，LR为0或1，某个结点的左或右子树。非空二叉树c与T不相交且右子树为空。根据LR为0或1，插入c为T中p指结点的左或右子树。P所指结点的原有左或右子树则成为c的右子树。

DeleteChild(T，p，LR)  删除子树  p指向T中某个结点，LR为0或1。根据LR为0或1，删除T中p所指结点的左或右子树。

6、二叉树的遍历

PreOrderTraverse(T，Visit())  前序遍历树visit是对结点操作的应用函数。先序遍历T，对每个结点调用函数visit()一次且仅一次。一旦visit()失败，则操作失败。

InorderTraverse(T，Visit())中序遍历树

PostOrderTraverse(T．Visit())候序遍历树

LeveleOrderTraverse(T，Visit())层次序遍历树

一棵树至少有一个结点，二叉树可是一棵空树。

对一棵树孩子的顺序是不重要的。

对二叉树只讲左右兄弟，不讲长次兄弟。

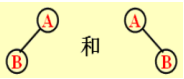
树与二叉树的表示和基本操作 - 数据结构 - 机器学习 

是两棵不同的二叉树。


来源：我是码农，转载请保留出处和链接！

本文链接：http://www.54manong.com/?id=199

(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646208", container: s }); })();
(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646147", container: s }); })();
window._bd_share_config={"common":{"bdSnsKey":{},"bdText":"","bdMini":"2","bdPic":"","bdStyle":"0","bdSize":"16"},"share":{},"image":{"viewList":["qzone","tsina","tqq","renren","weixin"],"viewText":"分享到：","viewSize":"16"},"selectShare":{"bdContainerClass":null,"bdSelectMiniList":["qzone","tsina","tqq","renren","weixin"]}};with(document)0[(getElementsByTagName('head')[0]||body).appendChild(createElement('script')).src='http://bdimg.share.baidu.com/static/api/js/share.js?v=89860593.js?cdnversion='+~(-new Date()/36e5)];
数据结构  

微信号：qq444848023    QQ号：444848023

加入【我是码农】QQ群：864689844（加群验证：我是码农）

<< 上一篇 下一篇 >>
(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646186", container: s }); })();
(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('
'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646175", container: s }); })();
搜索

网站分类

标签列表

最近发表

    (function(){ var bp = document.createElement('script'); var curProtocol = window.location.protocol.split(':')[0]; if (curProtocol === 'https'){ bp.src = 'https://zz.bdstatic.com/linksubmit/push.js'; } else{ bp.src = 'http://push.zhanzhang.baidu.com/push.js'; } var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(bp, s); })();

全站首页 | 数据结构 | 区块链| 大数据 | 机器学习 | 物联网和云计算 | 面试笔试

var cnzz_protocol = (("https:" == document.location.protocol) ? "https://" : "http://");document.write(unescape("%3Cspan id='cnzz_stat_icon_1276413723'%3E%3C/span%3E%3Cscript src='" + cnzz_protocol + "s23.cnzz.com/z_stat.php%3Fid%3D1276413723%26show%3Dpic1' type='text/javascript'%3E%3C/script%3E"));本站资源大部分来自互联网，版权归原作者所有！

jQuery(document).ready(function($){ /* prepend menu icon */ $('#daohangs-around').prepend('
'); /* toggle nav */ $("#caidan-tubiao").on("click", function(){ $("#daohangs").slideToggle(); $(this).toggleClass("active"); }); });

取消

感谢您的支持，我会继续努力的!

扫码支持
扫码打赏，你说多少就多少

打开支付宝扫一扫，即可进行扫码打赏哦

©著作权归作者所有：来自ZhiKuGroup博客作者没文化的原创作品，如需转载，请注明出处，否则将追究法律责任 来源：ZhiKuGroup博客，欢迎分享。

评论专区
  • 昵 称必填
  • 邮 箱选填
  • 网 址选填
◎已有 0 人评论
相关文章
搜索
作者介绍
superadmin

superadmin

30天热门
热评文章
最近发表
标签列表

©2012-2022 Think tank 鄂ICP备19030179号-1| 使用Chrome浏览本站最佳 | 声明：本站的文章和资源来自互联网或者站长的原创，按照 CC BY -NC -SA 3.0 CN协议发布和共享，转载或引用本站文章<应遵循相同协议。如果有侵犯版权的资源请尽快联系站长，我们会在24h内删除有争议的资源；本站所有收费以及免费的信息和数据仅供参考，不构成投资建议，本网站不承担由此导致的任何责任。 登陆

Powered By Z-BlogPHP

×
×
关闭广告
关闭广告
本站会员尊享VIP特权，现在就加入我们吧！登录注册×
»
会员登录
新用户注册
×
会员注册
已有账号登录
×