有趣的七桥问题，以及两种图的遍历方法

前记：这一章课件里主要讲了图及其衍生出来的森林、最小生成树等知识点。下面针对图的遍历举一个历史上有趣的问题“七桥问题”，后面还有一个图的两种遍历方法的C++实现，大家多熟悉一下。

一 题目描述：七桥问题Seven Bridges Problem，18世纪著名古典数学问题之一。在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点?

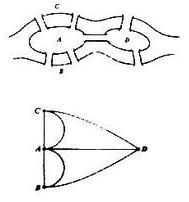
发展历程：

欧勒于1736年研究并解决了此问题，他把问题归结为如下右图的“一笔画”问题，证明上述走法是不可能的。

有关图论研究的热点问题。18世纪初普鲁士的柯尼斯堡，普雷格尔河流经此镇，奈发夫岛位于河中，共有7座桥横跨河上，把全镇连接起来。当地居民热衷于一个难题：是否存在一条路线，可不重复地走遍七座桥。这就是柯尼斯堡七桥问题。L.欧拉用点表示岛和陆地，两点之间的连线表示连接它们的桥，将河流、小岛和桥简化为一个网络，把七桥问题化成判断连通网络能否一笔画的问题。他不仅解决了此问题，且给出了连通网络可一笔画的充要条件是它们是连通的，且奇顶点(通过此点弧的条数是奇数)的个数为0或2。

当Euler在1736年访问Konigsberg, Prussia(now Kaliningrad Russia)时，他发现当地的市民正从事一项非常有趣的消遣活动。Konigsberg城中有一条名叫Pregel的河流横经其中，这项有趣的消遣活动是在星期六作一次走过所有七座桥的散步，每座桥只能经过一次而且起点与终点必须是同一地点。

Euler把每一块陆地考虑成一个点，连接两块陆地的桥以线表示。　

後来推论出此种走法是不可能的。他的论点是这样的，除了起点以外，每一次当一个人由一座桥进入一块陆地（或点）时，他（或她）同时也由另一座桥离开此点。所以每行经一点时，计算两座桥（或线），从起点离开的线与最後回到始点的线亦计算两座桥，因此每一个陆地与其他陆地连接的桥数必为偶数。

七桥所成之图形中，没有一点含有偶数条数，因此上述的任务无法完成.

欧拉的这个考虑非常重要，也非常巧妙，它正表明了数学家处理实际问题的独特之处——把一个实际问题抽象成合适的“数学模型”。这种研究方法就是“数学模型方法”。这并不需要运用多么深奥的理论，但想到这一点，却是解决难题的关键。

接下来，欧拉运用网络中的一笔画定理为判断准则，很快地就判断出要一次不重复走遍哥尼斯堡的7座桥是不可能的。也就是说，多少年来，人们费脑费力寻找的那种不重复的路线，根本就不存在。一个曾难住了那么多人的问题，竟是这么一个出人意料的答案！

1736年，欧拉在交给彼得堡科学院的《哥尼斯堡7座桥》的论文报告中，阐述了他的解题方法。他的巧解，为后来的数学新分支——拓扑学的建立奠定了基础。

七桥问题和欧拉定理。欧拉通过对七桥问题的研究，不仅圆满地回答了哥尼斯堡居民提出的问题，而且得到并证明了更为广泛的有关一笔画的三条结论，人们通常称之为欧拉定理。对于一个连通图，通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。

此题被人教版小学数学第十二册书收录.在95页。

此题也被人教版初中第一册收录．在一百二十一页．

一笔划：■⒈凡是由偶点组成的连通图，一定可以一笔画成。画时可以把任一偶点为起点，最后一定能以这个点为终点画完此图。

■⒉凡是只有两个奇点的连通图（其余都为偶点），一定可以一笔画成。画时必须把一个奇点为起点，另一个奇点终点。

■⒊其他情况的图都不能一笔画出。(奇点数除以二便可算出此图需几笔画成。)

二 题目：建立图的存储结构，输出深度遍历和广度遍历的结果。

C++语言描述的方法：

//图的遍历是指按某条搜索路径访问图中每个结点，使得每个结点均被访问一次，而且仅被访问一次。图的遍历有深度遍历算法和广度遍历算法，程序如下： 
#include <iostream>
#define INFINITY 32767
#define MAX_VEX 20 //最大顶点个数
#define QUEUE_SIZE (MAX_VEX+1) //队列长度
using namespace std;
bool *visited;  //访问标志数组
//图的邻接矩阵存储结构
typedef struct{
  char *vexs; //顶点向量
  int arcs[MAX_VEX][MAX_VEX]; //邻接矩阵
  int vexnum,arcnum; //图的当前顶点数和弧数
}Graph;
//队列类
class Queue{
  public:
  void InitQueue(){
    base=(int *)malloc(QUEUE_SIZE*sizeof(int));
    front=rear=0;
  }
  void EnQueue(int e){
    base[rear]=e;
    rear=(rear+1)%QUEUE_SIZE;
  }
  void DeQueue(int &e){
    e=base[front];
    front=(front+1)%QUEUE_SIZE;
  }
  public:
  int *base;
  int front;
  int rear;
};
//图G中查找元素c的位置
int Locate(Graph G,char c){
  for(int i=0;i<G.vexnum;i++)
  if(G.vexs[i]==c) return i;
  return -1;
}
//创建无向网
void CreateUDN(Graph &G){
  int i,j,w,s1,s2;
  char a,b,temp;
  printf("输入顶点数和弧数:");
  scanf("%d%d",&G.vexnum,&G.arcnum);
  temp=getchar(); //接收回车
  G.vexs=(char *)malloc(G.vexnum*sizeof(char)); //分配顶点数目
  printf("输入%d个顶点.\n",G.vexnum);
  for(i=0;i<G.vexnum;i++){ //初始化顶点
    printf("输入顶点%d:",i);
    scanf("%c",&G.vexs[i]);
    temp=getchar(); //接收回车 
  }
  for(i=0;i<G.vexnum;i++) //初始化邻接矩阵
    for(j=0;j<G.vexnum;j++)
      G.arcs[i][j]=INFINITY;
  printf("输入%d条弧.\n",G.arcnum);
  for(i=0;i<G.arcnum;i++){ //初始化弧
    printf("输入弧%d:",i);
    scanf("%c %c %d",&a,&b,&w); //输入一条边依附的顶点和权值
    temp=getchar(); //接收回车
    s1=Locate(G,a);
    s2=Locate(G,b);
    G.arcs[s1][s2]=G.arcs[s2][s1]=w;
  }
}
//图G中顶点k的第一个邻接顶点
int FirstVex(Graph G,int k){
  if(k>=0 && k<G.vexnum){ //k合理
    for(int i=0;i<G.vexnum;i++)
      if(G.arcs[k][i]!=INFINITY) return i;
  }
  return -1;
}
//图G中顶点i的第j个邻接顶点的下一个邻接顶点
int NextVex(Graph G,int i,int j){
  if(i>=0 && i<G.vexnum && j>=0 && j<G.vexnum){ //i,j合理
    for(int k=j+1;k<G.vexnum;k++)
      if(G.arcs[i][k]!=INFINITY) return k;
  }
  return -1;
}
//深度优先遍历
void DFS(Graph G,int k){
  int i;
  if(k==-1){ //第一次执行DFS时,k为-1
    for(i=0;i<G.vexnum;i++)
      if(!visited[i]) DFS(G,i); //对尚未访问的顶点调用DFS
  }
  else{ 
    visited[k]=true;
    printf("%c ",G.vexs[k]); //访问第k个顶点
    for(i=FirstVex(G,k);i>=0;i=NextVex(G,k,i))
      if(!visited[i]) DFS(G,i); //对k的尚未访问的邻接顶点i递归调用DFS
  }
}
//广度优先遍历
void BFS(Graph G){
  int k;
  Queue Q; //辅助队列Q
  Q.InitQueue();
  for(int i=0;i<G.vexnum;i++)
    if(!visited[i]){ //i尚未访问
      visited[i]=true;
      printf("%c ",G.vexs[i]);
      Q.EnQueue(i); //i入列
      while(Q.front!=Q.rear){
        Q.DeQueue(k); //队头元素出列并置为k
        for(int w=FirstVex(G,k);w>=0;w=NextVex(G,k,w))
          if(!visited[w]){ //w为k的尚未访问的邻接顶点
            visited[w]=true;
            printf("%c ",G.vexs[w]);
            Q.EnQueue(w);
          }
      }
    }
}
 
//主函数
void main(){
  int i;
  Graph G;
  CreateUDN(G);
  visited=(bool *)malloc(G.vexnum*sizeof(bool)); 
  printf("\n广度优先遍历: ");
  for(i=0;i<G.vexnum;i++)
  visited[i]=false;
  DFS(G,-1);
  printf("\n深度优先遍历: ");
  for(i=0;i<G.vexnum;i++)
  visited[i]=false;
  BFS(G);
  printf("\n程序结束.\n");
}

输出结果为（红色为键盘输入的数据，权值都置为1）：

输入顶点数和弧数:8 9

输入8个顶点.

输入顶点0:a

输入顶点1:b

输入顶点2:c

输入顶点3:d

输入顶点4:e

输入顶点5:f

输入顶点6:g

输入顶点7:h

输入9条弧.

输入弧0:a b 1

输入弧1:b d 1

输入弧2:b e 1

输入弧3:d h 1

输入弧4:e h 1

输入弧5:a c 1

输入弧6:c f 1

输入弧7:c g 1

输入弧8:f g 1

广度优先遍历: a b d h e c f g

深度优先遍历: a b c d e f g h

程序结束.

来源：我是码农，转载请保留出处和链接！

本文链接：http://www.54manong.com/?id=208

• 学习数据结构的意义和作用2018-09-03 22:48
• 数组操作2018-09-10 21:35
• 两个二叉树相关的常见题目2018-09-03 23:05
• 数据结构知识点总结（六）2018-09-10 21:21