如何在Python中创建简单的神经网络
神经网络(NN),也称为人工神经网络(ANN),是机器学习领域中学习算法的子集,其松散地基于生物神经网络的概念。
Andrey Bulezyuk是一位德国机器学习专家,拥有超过五年的经验,他说“神经网络正在彻底改变机器学习,因为它们能够有效地模拟各种学科和行业的复杂抽象。”
基本上,ANN包含以下组件:
接收数据并传递数据的输入层
隐藏层
输出层
层之间的权重
每个隐藏层的故意激活功能。在这个简单的神经网络Python教程中,我们将使用Sigmoid激活函数。
有几种类型的神经网络。在这个项目中,我们将创建前馈或感知神经网络。这种类型的ANN直接从前到后传递数据。
训练前馈神经元通常需要反向传播,这为网络提供了相应的输入和输出集。当输入数据被传输到神经元时,它被处理,并产生输出。
这是一个显示简单神经网络结构的图表:
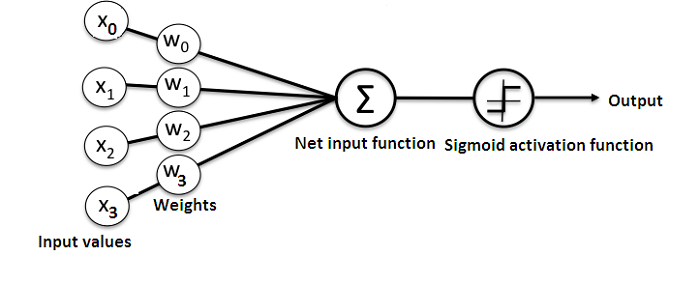
而且,理解神经网络如何工作的最好方法是学习如何从头开始构建一个(不使用任何库)。
在本文中,我们将演示如何使用Python编程语言创建一个简单的神经网络。
问题
这是一个显示问题的表。
| 输入 | 产量 | |||
| 培训数据1 | 0 | 0 | 1 | 0 |
| 培训数据2 | 1 | 1 | 1 | 1 |
| 培训数据3 | 1 | 0 | 1 | 1 |
| 培训数据4 | 0 | 1 | 1 | 0 |
| 新形势 | 1 | 0 | 0 | ? |
我们将训练神经网络,以便在提供一组新数据时可以预测正确的输出值。
正如您在表中看到的那样,输出的值始终等于输入节中的第一个值。因此,我们期望输出(?)的值为1。
让我们看看我们是否可以使用一些Python代码来提供相同的结果(在继续阅读之前,您可以在本文末尾仔细阅读此项目的代码)。
创建NeuralNetwork类
我们将在Python中创建一个NeuralNetwork类来训练神经元以提供准确的预测。该类还将具有其他辅助函数。
即使我们不会将神经网络库用于这个简单的神经网络示例,我们也会导入numpy库来协助计算。
该库带有以下四种重要方法:
EXP -用于产生所述自然指数
数组 - 用于生成矩阵
点 -用于矩阵相乘
随机 - 用于生成随机数。请注意,我们将对随机数进行播种以确保其有效分布。
应用Sigmoid函数
我们将使用Sigmoid函数,它绘制一个特征性的“S”形曲线,作为神经网络的激活函数。
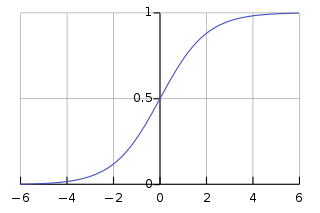
此函数可以将任何值映射到0到1之间的值。它将帮助我们规范化输入的加权和。
此后,我们将创建Sigmoid函数的导数,以帮助计算权重的基本调整。
可以使用Sigmoid函数的输出来生成其导数。例如,如果输出变量是“x”,那么它的导数将是x *(1-x)。
训练模型
这是我们将教导神经网络进行准确预测的阶段。每个输入都有一个权重 - 正面或负面。
这意味着具有大量正权重或大量负权重的输入将更多地影响所得到的输出。
请记住,我们最初开始时将每个权重分配给一个随机数。
以下是我们在此神经网络示例问题中使用的训练过程的过程:
我们从训练数据集中获取输入,根据它们的权重进行一些调整,并通过计算ANN输出的方法来虹吸它们。
我们计算了反向传播的错误率。在这种情况下,它是神经元预测输出与训练数据集的预期输出之间的差异。
根据得到的误差范围,我们使用误差加权导数公式进行了一些小的权重调整。
我们将这个过程重复15,000次。在每次迭代中,同时处理整个训练集。
我们使用“.T”函数将矩阵从水平位置转换到垂直位置。因此,数字将以这种方式存储:

最终,神经元的权重将针对所提供的训练数据进行优化。因此,如果使神经元考虑与前一个相同的新情况,则可以进行准确的预测。这就是反向传播的方式。
包起来
最后,我们初始化了NeuralNetwork类并运行了代码。
以下是如何在Python项目中创建神经网络的完整代码:
导入 numpy 为 npclass NeuralNetwork(): def __init __(self): #seeding for random number generation np.random.seed(1) 通过1点矩阵值#converting权重3从-1到1和0意味着 自 .synaptic_weights = 2 * np.random.random((3,1)) - 1 def sigmoid(self,x): #应用sigmoid函数 返回 1 /(1 + np.exp(-x)) def sigmoid_derivative(self,x): #computing为Sigmoid函数 返回 x *(1 - x) def train(self,training_inputs,training_outputs,training_iterations): #training模型进行准确的预测,同时连续调整权重 以进行范围内的迭代(training_iterations): #siphon训练数据通过neuron output = self .think(training_inputs) #computing反向传播的错误率 error = training_outputs - 输出 #performing weight adjustment adjustment = np.dot(training_inputs.T,error * self .sigmoid_derivative(output)) 自我 .synaptic_weights + =调整 def think(self,inputs): #通过神经元传递输入以获得输出 #converting值到浮点数 inputs = inputs.astype(float) output = self .sigmoid(np.dot(inputs,self .synaptic_weights)) 返回输出if __name__ == “ __ main__ ”: #initializing神经元类 neural_network = NeuralNetwork() print(“Beginning Randomly Generated Weights:”) print(neural_network.synaptic_weights) #training数据由4个实例- 3个输入值和1个输出 training_inputs = np.array([[ 0,0,1 ], [ 1,1,1 ], [ 1,0,1 ], [ 0,1,1 ]]) training_outputs = np.array([[ 0,1,1,0 ]]):T #training发生Neural_network.train (training_inputs,training_outputs,15000) 打印(“训练结束后的重量:”) 打印(neural_network.synaptic_weights) user_input_one = str(输入(“用户输入一:”)) user_input_two = str(输入(“用户输入二:”)) user_input_three = str(输入(“用户输入三:”)) print(“考虑新情况:”,user_input_one,user_input_two,user_input_three) print(“新输出数据:”) print(neural_network.think(np.array([user_input_one,user_input_two,user_input_three]))) print(“哇,我们做到了!“)
以下是运行代码的输出:
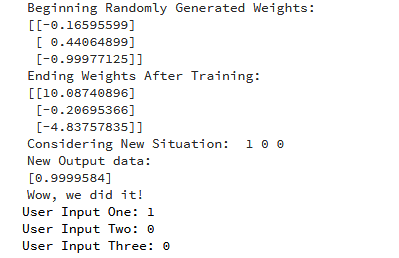
我们设法创建了一个简单的神经网络。
神经元开始为自己分配一些随机权重。此后,它使用训练样例训练自己。
因此,如果出现新情况[1,0,0],则其值为0.9999584。
你记得我们想要的正确答案是1吗?
然后,这非常接近 - 考虑到Sigmoid函数输出0到1之间的值。
当然,我们只使用一个神经网络来执行简单的任务。如果我们将数千个这些人工神经网络连接在一起怎么办?我们可以模仿人类思维如何100%运作吗?
有什么评价或者疑问吗?
请在下面提供。
Bio:Michael J. Garbade博士是洛杉矶区块链教育公司LiveEdu的创始人兼首席执行官。它是世界领先的平台,为人们提供在未来技术领域(包括机器学习)中创建完整产品的实用技能。






评论专区