贝叶斯定理:数据科学的圣杯
贝叶斯定理可能是数理统计和概率论领域最重要的定理。出于这个原因,该定理经常在数据科学领域中得到应用。
在本文中,我将使用实际问题直观地推导出贝叶斯定理。

0.简介
以18世纪英国数学家托马斯贝叶斯命名的B ayes定理是确定条件概率的数学公式。该定理在数据科学领域具有重要意义。例如,贝叶斯定理的许多应用之一是贝叶斯推理,这是统计推断的一种特殊方法。
贝叶斯推理是一种方法,其中贝叶斯定理用于在更多证据或信息可用时更新假设的概率。贝叶斯推理在广泛的活动,包括已发现的应用科学,工程,哲学,医学,体育,和法律。
例如,在金融领域,贝叶斯定理可用于评估向潜在借款人提供贷款的风险。在医学中,该定理可用于通过考虑任何给定的人患病的可能性和测试的一般准确性来确定医学测试结果的准确性。
让我们现在变得实用......
2.问题陈述
C旁边有两个碗X和Y,里面装满了橘子和蓝莓。在这种情况下,您确切地知道两个碗中每个碗中有多少橙子和蓝莓。
如果我问你从碗X中挑选橙子的可能性有多大,你可以确切地说出概率。由于碗X中有11个项目,其中3个是橙色,因此挑选橙色的概率为p(橙色) = 3/11。
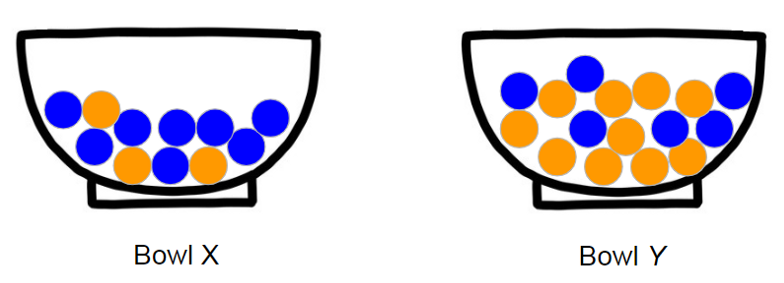
碗X和碗Y充满橙子和蓝莓。
反转案例

但是如果我从随机碗中挑选一件物品会发生什么。让我们说我选了一个蓝莓。你能说出蓝莓从哪个碗里挑出的概率吗?
这是使用贝叶斯定理可以回答的问题。
3.贝叶斯定理推导
为了得出贝叶斯定理,我们将模拟一个实验。在这个实验中,我们掷骰子。每当骰子显示数字3或更少时,我们将从碗X中挑选一个项目,对于数字4或更高,我们将从碗Y中挑选一个项目。我们要做N = 300次。为了简化问题,我们引入了以下缩写:
蓝莓:= B,橙色:= O,碗X:= X,碗Y:= Y.
在我们掷骰子N = 300次之后,我们将获得关于从两个碗中挑选的物品数量的一些统计结果。该实验的假设结果如图1所示。这里s代表碗或从中挑选物品的“来源”。y是可观察变量(蓝莓或橙色)。
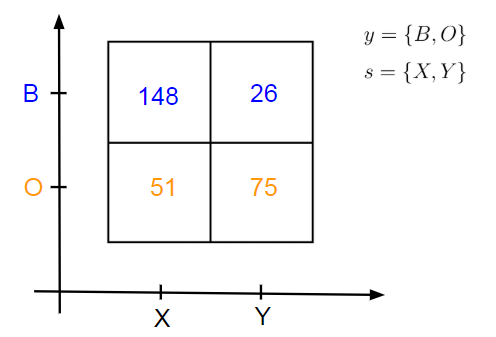
这个数字告诉我们,我们选择了......
......来自碗X的蓝莓的148倍:n(s = X,y = B)= 148
...来自碗Y的蓝莓的26倍:n(s = Y,y = B)= 26
... 51倍从碗X橙色:N(S = X,Y = ö)= 51
... 75倍从碗ÿ橙色:N(S = Ý,Y = ö)= 75
鉴于这些统计数字,我们现在可以提出一些有趣的问题......
从碗X中挑选随机物品的概率是多少?
获得我们表示为p(s = X)的概率,我们必须将仅从碗X中挑选的项目数除以总选数的数量N = 300。这是n(s = X,y = B)= 148从X中选取的蓝莓数量和n(s = X,y = O)= 51从X中挑选的橙子数量。因此,选择任何项目的概率从X看起来如下:
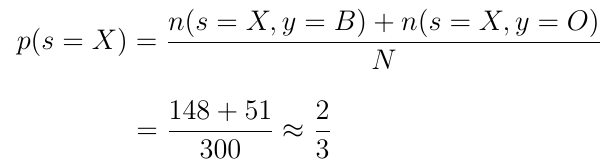
注意:这种概率称为“先验概率”。在贝叶斯统计推断中,先验概率是在收集新数据之前事件的概率。在这种情况下,p(s = X)表示从X中拾取项目的概率,而不知道它是哪个项目。
因此,从Y中选择项目的概率p(s = Y)是:
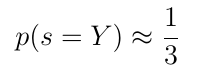
挑选橙子/蓝莓的概率是多少?
这次我们想知道在不考虑特定碗的情况下挑选橙子或蓝莓的可能性。我们将这些概率表示为p(y = 0)和p(y = B)。计算与前一种情况类似。我们将特定项目的选秀数除以总选秀权数。得到的概率由方程式给出。3和Eq。4:
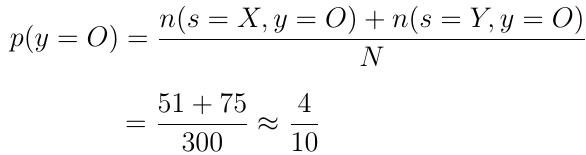
从X中挑选蓝莓的概率是多少?
现在我们将计算联合概率p(s = X,y = B),它告诉我们从X中采摘蓝莓的可能性。
注意:联合概率是事件Nr.1在同一事件Nr发生的概率。2发生。在这种情况下,一个事件是从碗中挑选恰好是X的。另一个事件是我们选择了一个蓝莓。
为了计算联合概率,我们需要将我们从X中挑选蓝莓的次数除以总数:
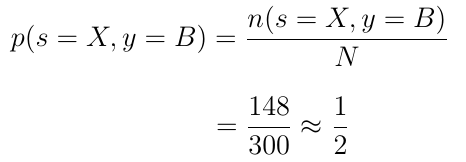
因此,从Y采摘蓝莓的概率是:

从X中挑选橙色
的概率是:

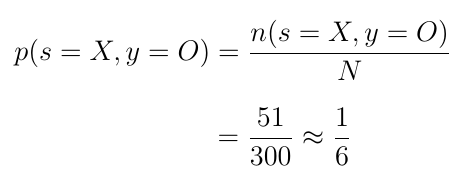
鉴于我们从X中挑选出来,它是蓝莓的概率是多少?
现在它变得有趣了。我们计算第一个条件概率。在这种情况下,我们确定我们从哪个碗中挑选。在这种情况下,我们说,我们从X中选择。根据这些知识,我们可以计算出告诉我们选择蓝莓的可能性的概率。
该条件概率表示为p(y = B | s = X),s = X是我们从X中选择项目的条件。为了计算P(Y = B | S = X)我们需要划分的我们已经拾取从蓝莓次数X从由拾取物品的总数X:
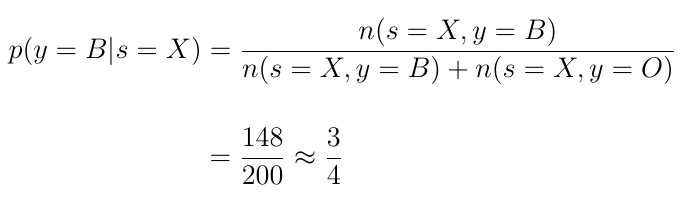
产品规则
现在是第一个重要统计规则的时候了。这里我们采用先前导出的概率从X p(s = X,y = B)中挑选蓝莓,并通过将其乘以(n(s = X,y = B)+ n(s = X,y = )来扩展该等式O))在分母和分子中。我们可以这样做,因为概率p(s = X,y = B)的值不会被此扩展名改变。
现在,如果你仔细研究一下这个等式,你会注意到p(s = X,y = B)的新表达式由两个其他概率p(y = B | s = X)和p之间的乘积组成( s = X)我们之前得到的。
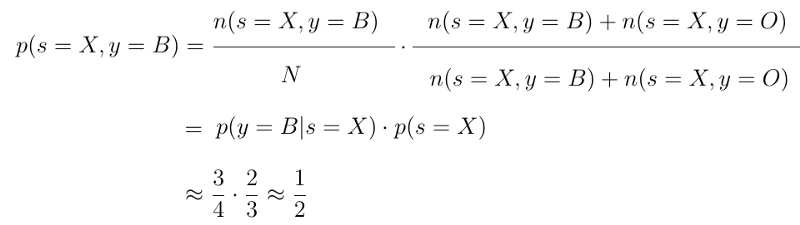
概率之间的这种关系称为产品规则。乘积规则允许我们通过使用条件概率p(y = B | s = X)和先验概率p(s = X)来计算联合概率p(s = X,y = B )。
求和规则
现在让我们重新审视先验概率p(s = X),这使我们有可能从X中挑选任何项目。如果将方程式除以两个加数,如公式2中的第二行所示。你可以观察到这两个加法只不过是我们之前得出的两个联合概率。
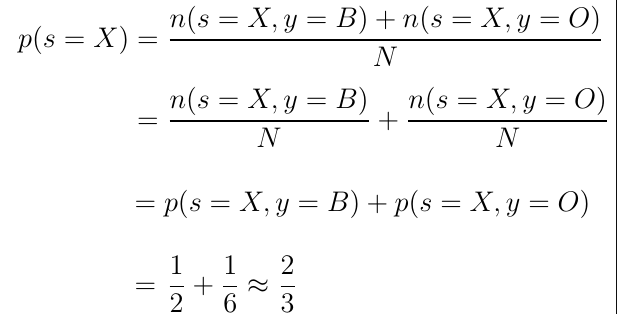
这种关系称为求和规则。求和规则允许通过对包含来自先前和任何其他随机变量y的随机变量s = X的联合概率求和来计算先验p(X)概率。
贝叶斯规则
对于产品规则,关节中随机变量的顺序无关紧要。因此p(s,y)和p(y,s)具有相同的值。
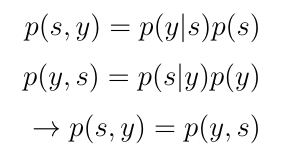
如果我们将值p(s,y)和p(y,s)等同并进行一些重组,我们得到p(s | y)的新数学表达式。p(s | y)的这个新表达式是贝叶斯规则。
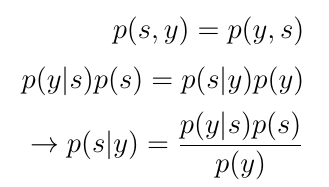
最后:从哪个碗里取出蓝莓?
贝叶斯定理为我们提供了计算条件概率p(s | y)的公式,这是我们最初问题的答案。
我们选择蓝莓的事实可以用条件y = B来表示。要回答这些碗是蓝莓采摘从我们必须计算问题P(S | Y = B)为S = X和S =ÿ。p(s | y)的两个值都告诉我们从碗X或碗Y中采摘蓝莓的可能性。
让我们做了计算S = X。幸运的是,我们需要的所有概率,我们已在前面的部分中计算过。如果我们将这些概率插入到方程式中的p(s = X | y = B)中。我们得出以下结论:鉴于我们选择了蓝莓,从碗X中采摘这种蓝莓的概率约为85%。对于任何其他情况,可以类似地进行计算。
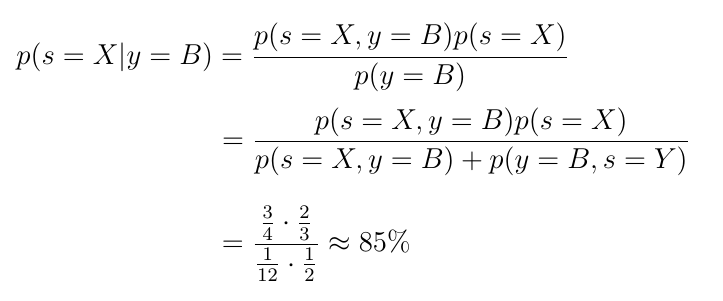
没有贝叶斯定理,p(s | y)的计算将非常困难。然而,该定理允许我们使用可以用更少的努力计算的概率来计算该概率。这是贝叶斯定理的神奇之处:难以计算的概率分布由非常容易计算的概率表示。
特别声明:有一个在线课程即将推出!
我们真的很接近完成我们期待已久的“ 预测分析深度学习 ”课程。该课程的重点是在Predictive Analytics领域构建深度学习应用程序,并使其在生产环境中运行。通常不被其他在线课程覆盖的技能组合 - 但对于那些希望在这一领域专业工作的人来说至关重要。
如果您有兴趣在课程发布时收到通知或收到更多详细信息,您可以订阅以下时事通讯 - 很好!
PS:同样通过订阅,您可以获得一个有限的地方和50%的折扣。
原文链接:https://towardsdatascience.com/bayes-theorem-the-holy-grail-of-data-science-55d93315defb






评论专区