密码学概述

密码学起源于数千年以前，最早可追溯到古巴比伦时代，作为保护信息传输的技术手段，最早应用于军事、外交和情报领 域。在20世纪70年代之前，密码学大都属于政府的应用范畴。有两件事的发生将密码学带入了公众领域：标准加密系统——数据加密标准（Data Encryption Standard，DES）的诞生和公钥加密算法（也称为非对称加密算法）的发明[1]。

密码学伴随着密码分析学的发展而发展。按算法思想的革新可划分为3大阶段：古典密码学、现代密码学和公钥密码学。 1949年以前的密码学统称为古典密码学，它的安全基于加密算法的保密性。1949年，香农（Shannon）发表了《保密系统的通信理论》一文，文中的 信息论为对称密码系统建立了理论基础，密码学开始成为一门科学。基于密钥安全而非加密算法安全的理论与技术变革，成为密码学发展的一个新的里程碑，标志着 现代密码学时代的来临。1976年，Whitfield Diffie和Martin Hellman首次提出了基于数学难题的公钥密码机制；1978年，RSA公钥密码机制出现，它成为公钥密码的杰出代表并成为事实标准，这在密码学史上创 造了又一个新的里程碑。20世纪90年代，公钥密码学进一步发展，基于椭圆曲线乘法、素数幂等数学函数的公钥算法诞生，这使得数字密钥和不可伪造的数字签 名成为可能。

如今密码学相关技术已经深入各个领域，它们的理论共识都遵循由奥古斯特·柯克霍夫在19世纪提出的“柯克霍夫原 则”——密码系统应该就算被所有人知道其运作步骤，它仍然是安全的。即算法是公开的，唯一需要保护的是密钥。密码学算法的安全性被攻破有两个可能：一是算 法本身的漏洞，不需要密钥即可以破解算法；二是在可接受的时间范围内暴力破解。

1.古典密码学

古典密码学历史悠久，时间跨越了两三千年。它主要应用于军事、外交和情报领域。它的安全性是基于算法的，类似于目前经常用的编码算法。古典密码编码算法归根结底主要有两种：置换和代换。

把明文字符串中的字母重新排列，字母本身不变，位置却改变了，由此编成的密码称为置换密码。最简单的置换密码是把 明文中的字母倒序排列，然后截成固定长度的字母组作为密文。代换密码则是将明文中的字符替代成其他字符，比如古罗马凯撒密码是将明文中的所有字母都在字母 表上向后（或向前）按照一个固定数目进行偏移，得到的新数据就是密文。位数就是凯撒密码加密和解密的密钥。

古典密码学大都比较简单，主要采用手工或机械操作来实现加解密，而算法是基于字符串的，由于古典密码学的安全性主要是依赖于算法的保密性，所以整体安全性不高。

2.现代密码学

1949年以香农的信息论诞生为标志，密码学的发展进入了第二个阶段。现代计算机科学与信息技术的蓬勃发展，使得 基于复杂计算的密码学成为可能。同时密码学首次成为一门科学。加密算法开始时是基于密钥来进行信息的加解密，通过密钥加密明文并主要以二进制的形式进行传 输。通常情况下，密钥越长，代表着密文被破解的难度越大。由于加密算法和解密算法都是同一模式，同时只用一把密钥保证加密数据的安全，因此这种加密算法也 叫作“对称加密算法”。

对称加密有一个最大的弱点：甲方必须把密钥告诉乙方，否则乙方无法解密。而保存和传递密钥，就成了最头疼的问题。

这个时间段是密码学开始蓬勃发展的一个开端，后期发展出来的公钥密码学、哈希算法、其实属于现代密码学的范畴。

3.公钥密码学

相比1976年以前的密码学思想，公钥密码学可以在不直接传递密钥的情况下，完成密文的解密。这个算法机制启发了 其他科学家，人们认识到，加密和解密可以使用不同的规则，只要这两种规则之间存在某种对应关系即可，这样就避免了直接传递密钥。基于这种公钥机制的思想， 开始出现了一系列非对称加密算法。

下图比较说明了非对称加密算法与对称加密算法的区别。

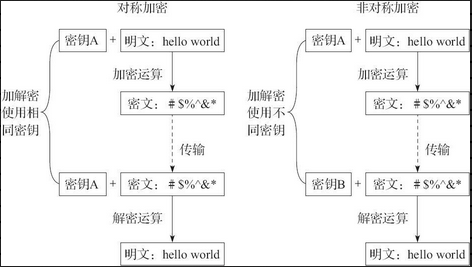
非对称加密需要两个（一对）密钥：公开密钥（Publickey）和私有密钥（Privatekey），用公钥对数据进行加密后，只有对应的私钥才能解密；反之，如果私钥用于加密，则只有对应的公钥才能解密。通信双方无须交换密钥，就可以建立保密通信。

公钥密码体制根据其所依据的数学难题一般分为3类：大整数分解问题类、离散对数问题类、椭圆曲线类[2]。

4.哈希算法

哈希函数（Hash Function）也称为散列函数，是能计算出一个数字消息所对应的、长度固定的字符串（又称消息摘要）的算法。给定一个输入x，它会算出相应固定长度的输出H（x）。哈希函数的主要特征是：

1）输入x可以是任意长度的字符串。

2）输出结果，即H（x）的长度是固定的。

3）计算H（x）的过程是高效的（对于长度为n的字符串x，计算出H（x）的时间复杂度应为O（n）），同时H（x）要相对易于计算，可通过硬件和软件实现。

而对于比特币加密系统使用的哈希函数，它需要额外具备以下的性质：

1）免碰撞，即不会出现输入x≠y但是H（x）=H（y）的情况，也就是强抗冲突性。

2）隐匿性，也就是说，对于一个给定的输出结果H（x），想要逆推出输入x，在计算上是不可能的。

3）不存在比穷举更好的方法，以使哈希结果H（x）落在特定的范围。

区块链中的密码学

在比特币区块链的整个体系中，大量使用了公开的加密算法，比如Merkle Tree哈希树算法、椭圆曲线算法、SHA-256哈希算法、对称加密算法以及一些编码算法，如Base58编码、VarInt编码、DER编码等。下面我们来了解其中的几个核心算法。

1.椭圆曲线算法

椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。它的主要优势是：在某些情况下，它比其他的算法（比如RSA）使用更小的密钥，但提供相当的或更高等级的安全性。

比特币使用了基于secp256k1椭圆曲线数学的公钥密码学算法。它包含私钥与公钥，交易发出方用私钥进行签名，并将签名与原始数据发送给整个比特币网络，网络中的所有节点则用公钥对交易有效性进行验证。签名算法保证了交易是由拥有对应私钥的人所发出的。

数据签名算法的核心在于证明数据是签名者发出的、不可抵赖的，而不是待签名数据本身的保密性。

2.SHA-256哈希算法

SHA是安全散列算法（Secure Hash Algorithm）的缩写，是一个密码散列函数家族。这一组函数是由美国国家安全局（NSA）设计，美国国家标准与技术研究院（NIST）发布的，包括 SHA-1、SHA-224、SHA-256、SHA-384和SHA-512五种变体，主要适用于数字签名标准。后4个哈希函数又并称为SHA-2。

SHA-1在许多安全协议中广为使用，包括TLS、SSL、PGP、SSH、S/MIME和IPsec，曾被视为 是MD5（更早之前被广为使用的哈希函数）的后继者。但随着计算机技术的发展，SHA-1的安全性被密码学家严重质疑，且在2005年被王小云等密码学家 成功破译。SHA-2的算法跟SHA-1基本相似，但至今尚未出现对SHA-2的有效攻击，安全性较高。SHA-256就是SHA-2函数中的一个，是输 出值为256位的哈希算法。

3.对称加密算法

AES（Advanced Encryption Standard）是一个对称分组密码算法，旨在取代DES成为广泛使用的标准，最终成为美国新的数据加密标准而被广泛应用在各个领域。其大致运作原理和前文的对称加密算法的流程相同。

比特币官方客户端[3]使用AES算法中的AES-256-CBC来加密钱包文件，用户设置密码后，采用用户设置的密码通过AES算法对钱包私钥进行加密，确保客户端私钥的安全，从而保证资产的安全。

4.Base58编码

可读性编码算法在理论上并非密码学理论的核心内容，它类似于古典密码学里的置换算法机制。编码算法的目的不是为了保护数据的安全性，而是为了可读性。

信息以二进制的形式传输，不具备可读性，而数字与字母组成的字符串才更容易被识别。可读性编码不改变信息内容，只改变信息内容的表现形式，部分编码算法还加入了容错校验功能，以保证传输过程中数据的准确性和完整性。

Base58是比特币使用的一种独特的编码方式，主要用于产生比特币的钱包地址。相比Base64，Base58不使用数字“0”、大写字母“O”、大写字母“I”和小写字母“l”，以及“+”和“/”符号[4]。

设计Base58的主要目的是：

1）避免混淆。在某些字体下，数字0和大写字母O，以及大写字母I和小写字母l非常相似。

2）不使用“+”和“/”的原因是，非字母或数字的字符串作为账号的一部分被接受。

3）没有标点符号，通常不会被从中间分行。

4）大部分的软件支持双击选择整个字符串。

比特币使用了Base58算法来对公钥的Hash160及私钥进行编码，从而生成以1或3开头的比特币地址及WIF（Wallet Import Format）格式的私钥。

[1] 引用自https://en.wikipedia.org/wiki/History_of_cryptography。

[2] 也有人把椭圆曲线类归为离散对数类。

[3] 引用自https://bitcoin.org/en/download。

[4] 引用自https://zh.wikipedia.org/wiki/Base58。

来源：我是码农，转载请保留出处和链接！

本文链接：http://www.54manong.com/?id=673

• 赋予公民权利，服务自己，服务他人2018-09-04 22:47
• 开启全新的金融信任时代2018-09-25 16:13
• 区块链在认证领域的应用前景2018-09-21 10:21
• 技术创新：从比特币到区块链2018-09-27 17:08