密码哈希函数是一类数学函数，可以在有限合理的时间内，将任意长度的消息压缩为固定长度的二进制串，其输出值称为哈希 值，也称为散列值。以哈希函数为基础构造的哈希算法，在现代密码学中扮演着重要的角色，常用于实现数据完整性和实体认证，同时也构成多种密码体制和协议的 安全保障。

碰撞是与哈希函数相关的重要概念，体现着哈希函数的安全性，所谓碰撞是指两个不同的消息在同一个哈希函数作用下，具有相同的哈希值。哈希函数的安全性是指在现有的计算资源（包括时间、空间、资金等）下，找到一个碰撞是不可行的。

在比特币系统中使用了两个密码学哈希函数，一个是SHA256，另一个是RIPEMD160。RIPEMD160主要用于生成比特币地址，我们着重分析比特币中用得最多的SHA256算法。

SHA256属于著名的SHA家族一员。SHA（Secure Hash Algorithm，安全哈希算法）是一类由美国国家标准与技术研究院（NIST）发布的密码哈希函数。正式名称为SHA的第一个成员发布于1993年， 两年之后，著名的SHA-1发布，之后另外的4种变体相继发布，包括SHA224、SHA256、SHA384和SHA512，这些算法也被称作 SHA2。SHA256算法是SHA2算法簇中的一类。对于长度小于264 位的消息，SHA256会产生一个256位的消息摘要。SHA256具有密码哈希函数的一般特性。

SHA256是构造区块链所用的主要密码哈希函数。无论是区块的头部信息还是交易数据，都使用这个哈希函数去计算相关 数据的哈希值，以保证数据的完整性。同时，在比特币系统中，基于寻找给定前缀的SHA256哈希值，设计了工作量证明的共识机制；SHA256也被用于构 造比特币地址，即用来识别不同的用户。

SHA256是一个Merkle-Damgard结构的迭代哈希函数，其计算过程分为两个阶段：消息的预处理和主循 环。在消息的预处理阶段，主要完成消息的填充和扩展填充，将所输入的原始消息转化为n个512比特的消息块，之后对每个消息块利用SHA256压缩函数进 行处理，SHA256的计算流程如图4-1所示。这个计算流程是一个迭代计算的过程，当最后1个消息块（第n块）处理完毕以后，最终的输出值就是所输入的 原始消息的SHA256值。

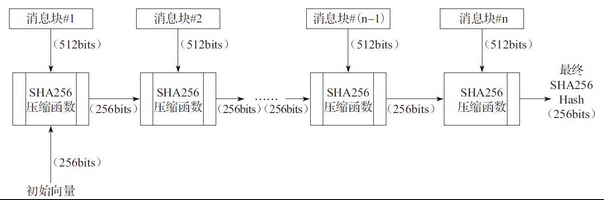
图4-1　SHA256计算流程

在比特币系统中，SHA256算法的一个主要用途是完成PoW（工作量证明）计算。按照比特币的设计初衷，PoW要求 钱包（节点）数和算力值大致匹配，因为需要通过CPU的计算能力来进行投票。然而随着人们对SHA256的计算由CPU逐渐升级到GPU，到FPGA，直 至到ASIC矿机，这使得节点数和PoW算力也渐渐失配。解决这个问题的一个思路是引入另外的一些哈希函数来实现PoW。

scrypt算法最早用于基于口令的密钥生成，该算法进行多次带参数的SHA256计算，即基于SHA256的消息认 证码计算，这类计算需要大量的内存支持。采用scrypt算法进行PoW计算，将PoW计算由已有的拼算力在一定程度上转化为拼内存，能够使得节点数和 PoW的计算力的失配现象得到缓解。莱特币就是采用scrypt算法完成PoW计算的。

SHA3算法是2012年10月由NIST所选定的下一代密码哈希算法。在遴选SHA3算法过程中人们提出了一系列的 候选算法，包括了BLAKE、Grostl、JH、Keccak、Skein、ECHO、Luffa、BMW、CubeHash、SHAvite、 SMID等，最后胜出的是Keccak算法。达世币（DASH，原名暗黑币，DarkCoin）定义了顺序调用上述11个哈希算法的X11算法，并利用这 个算法完成PoW计算。同样，由于采用了X11算法，使得节点数和PoW的计算力能够保持一定程度上的匹配。

4.1.1　哈希函数的性质与应用

我们来看看密码学哈希函数的3个主要性质及其应用。

1.抗碰撞性

如前所述，碰撞是与哈希函数相关的重要概念，所谓碰撞是指两个不同的消息在同一个哈希函数作用下，具有相同的哈希值。 哈希函数H的抗碰撞性是指寻找两个能够产生碰撞的消息在计算上是不可行的。值得注意的是找到两个碰撞的消息在计算上不可行，并不意味着不存在两个碰撞的消 息。由于哈希函数把大空间上的消息压缩到小空间上，碰撞肯定存在。例如，如果哈希值的长度固定为256位，显然如果顺序取1，2，…，2256 +1这2256 +1个输入值，逐一计算其哈希值，肯定能够找到两个输入值，使得它们的哈希值相同。

一般，依据生日悖论，如果随机挑选其中的2130 +1个输入，则有99.8%的概率可以发现至少一对碰撞的输入。然而，这样的计算非常耗时以至于计算不可行。对于哈希值长度为256位的哈希函数，要找到碰撞对，平均需要完成2128 次哈希计算，如果计算机每秒能够进行10000次哈希计算，则需要约1027 年才能完成这2128 次哈希计算。

哈希函数的抗碰撞（collition-resistance）特性常被用来进行完整性验证。完整性是信息安全的3个 基本要素之一，是指传输、存储信息的过程中，信息不被未授权的篡改或篡改后能被及时发现。由于哈希函数的抗碰撞性，我们可以把哈希值作为原输入消息的指纹 （因为很难找到另一个消息经哈希运算之后得到相同的哈希值）。如果原消息在传输过程中被篡改，那么运行哈希函数后得到的新哈希值就会和原来的哈希值不一 样，这样很容易就能发现消息在传输过程中完整性受损。对区块链来说，哈希函数的抗碰撞性可以用来做区块和交易的完整性交易。在区块链中，某个区块的头部信 息中会存储着前一个区块的信息的哈希值，如果能拿到前一个区块的信息，任何用户都可以比对计算出来的哈希值和存储的哈希值，来检测前一个区块的信息的完整 性。

2.原像不可逆

原像不可逆通俗地说，指的是知道输入值，很容易通过哈希函数计算出哈希值；但知道哈希值，没有办法计算出原来的输入 值。哈希函数的原像是不可逆的，这意味着依据哈希函数的输出是不能计算出该哈希函数的输入的，即已知H（m），试图计算出原始的m的值在计算上是不可行 的。更特别地，若对消息m进行哈希计算时，引入一个随机的前缀r，依据哈希值H（r||m），难以恢复出消息m，这代表着该哈希函数值隐藏了消息m。

承诺方案（Commitment Scheme）被认为是密码学领域中一类重要的密码学基本模型，承诺（Commitment）具有隐藏性和保密性。承诺模型可以看作一个密封信件的数字等 价体。如果Alice想承诺某个信息m，则她可把m放入一个密封的信封内，而无论什么时候她想公开这个信息，则只需要打开信封。这个过程要求数字信件能够 隐藏信息，即承诺的隐藏性，同时Alice也不能改变m；而通过承诺的打开，任何人都能验证他所得到的m其实就是Alice最初承诺的信息m，即承诺的绑 定性。

承诺方案包含以下两个算法。

·承诺值计算commit（m，r）：输入消息m和随机值r，返回承诺值c（=commit（m，r））。

·承诺验证verify（c，m，r）：输入承诺c，消息m和随机值r，若c==commit（m，r），返回真，否则返回假。

显然，如果定义commit（m，r）=H（r||m），利用哈希函数H的抗碰撞性和原像不可逆，承诺的隐藏性和绑定性均能成立，可以实现承诺方案。

3.难题友好性

通俗地说，难题友好性（Puzzle Friendliness）指的是没有便捷的方法去产生一满足特殊要求的哈希值。正式的定义是：一个哈希函数H称为难题友好的，如果对于每个n位的输出 y，若k是从一个具有较高不可预测性（高小熵，英文为high min-entropy）分布中选取的，不可能以小于2n 的时间找到一个x，使H（k||x）=y。这意味着如果有人想通过锁定哈希函数来产生一些特殊的输出y，而部分输入值以随机方式选定，则很难找到另外一个值，使得其哈希值正好等于y。

考虑一个由哈希函数构成的解谜问题：已知哈希函数H，一个高小熵分布的值value以及目标范围Y，寻找x，使得H（value||x）∈Y。

这个问题等价于需要找到一个输入值，使得输出值落在目标范围Y内，而Y往往是所有的输出值的一个子集。实际上，如果一个哈希函数H的输出为n位，那么输出值可以是任何一个0~2n 范围内的值。预定义的目标范围Y的大小决定了这个问题的求解难度。如果Y包含所有n比特的串，那么这个问题就简单平常了；但如果Y只包含一个元素，那么这 个求解是最难的，相当于给定一个哈希值，找出其中的一个原像。事实上，由于value具有高小熵分布，这确保了除了随机尝试x值以完成搜寻那个很大的空间 外，没有其他有效的途径了。

提示：小熵（min-entropy）是信息理论中衡量某个结果的可预测性的一个指标。高小熵指的是变量呈均 匀分布（随机分布）。如果我们从对分布的值进行随机抽样，不会经常抽到一个固定的值。例如，如果在一个128位的数中随机选一个固定的数n，那么选到该数 的几率是1/2128 。

哈希函数的难题友好性构成了基于工作量证明的共识算法的基础。例如，给定字符串“blockchain”，并在这个字 符串后面连接一个整数值串x，对连接后的字符串进行SHA256哈希运算，要求得到的哈希结果（以十六进制的形式表示）以若干个0开头的。按照这个规则， 由x=1出发，递增x的值，我们需要经过2688次哈希计算才能找到前3位均为0的哈希值，而要找到前6位均为0的哈希值，则需进行620969次哈希计 算。也就是说，没有更快捷的方法来产生一个满足要求的哈希结果。这样通过哈希运算得出的符合特定要求的哈希值，可以作为共识算法中的工作量证明。

4.1.2　哈希指针链

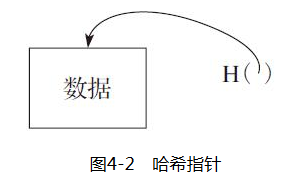
哈希指针是一类数据结构，除了包含通常的指针外，还包含一些数据信息以及与这些信息相关的密码哈希值，这就使得正常的指针可用于取回信息，哈希指针用于验证信息是否发生改变，图4-2表示了一个哈希指针。

区块链就可以看作一类使用哈希指针的链表，如图4-3所示。这个链表链接一系列的区块，每个区块包含数据以及指向表中前一个区块的指针。区块链中，前一个 区块指针由哈希指针所替换，因此每个区块不仅仅告诉前一个区块的位置，也提供一个哈希值去验证这个区块所包含的数据是否发生改变。

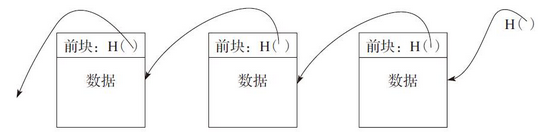
图4-3　哈希指针链

我们可以使用区块链去构造一个防篡改的日志系统。在这个系统中，基于区块链的日志节点链表被用来存储数据，链表节点通 过哈希指针链接，新节点追加在日志链表的尾部。同时，日志链表的头哈希指针所指向的头节点内容不可改变。若日志链表中的某个节点的数据被篡改，则系统能够 检测出来。

不妨假定攻击者改变了节点k的数据，由于其后继节点k+1存储了节点k的哈希值，由于密码哈希函数的抗碰撞性，通过简 单地计算节点k的数据的哈希值，就能发现计算出的值与节点k+1的哈希指针值不一致，于是可以断定节点k或节点k+1的信息被篡改。当然，攻击者可能能够 连续改变前一个节点的哈希值来掩盖不同，但这个策略在处理日志链表的头节点时将会失败。特别地，一旦我们将链表头部的哈希指针存储在不能改变的地方，攻击 者将不能改变任何节点而不被发觉。

因此，若攻击者想在日志链表中的任意位置改变数据，为保持一致性，他必须向表头方向修改所有的哈希指针，最终由于不能改变链表头部而失败。因此，只需单个哈希指针，基本上就能保证整个链表的哈希值的一致性，从而达到防篡改的目的。

来源：我是码农，转载请保留出处和链接！

本文链接：http://www.54manong.com/?id=1024

• 第2章 区块链式信用是如何渗透的2018-09-14 13:37
• 区块链在预测市场领域的应用前景2018-09-21 10:19
• 3.13　全局可用变量2018-09-17 16:15
• 3.7　其他场景2018-09-30 10:49