5.1 拜占庭容错技术 - 数据结构 - 机器学习
数据结构 - 机器学习
深度学习

当前位置:首页 » 区块链精品文章 » 正文
5.1 拜占庭容错技术
1454 人参与 2018年09月30日 14:48 分类 : 区块链精品文章 评论
拜占庭容错技术(Byzantine Fault Tolerance,BFT)是一类分布式计算领域的容错技术。拜占庭假设是对现实世界的模型化,由于硬件错误、网络拥塞或中断以及遭到恶意攻击等原因, 计算机和网络可能出现不可预料的行为。拜占庭容错技术被设计用来处理这些异常行为,并满足所要解决的问题的规范要求。
5.1.1 拜占庭将军问题
拜占庭容错技术来源于拜占庭将军问题。拜占庭将军问题是Leslie Lamport在20世纪80年代提出的一个假象问题[1] 。拜占庭是东罗马帝国的首都,由于当时拜占庭罗马帝国国土辽阔,每支军队的驻地分隔很远,将军们只能靠信使传递消息。发生战争时,将军们必须制订统一的行 动计划。然而,这些将军中有叛徒,叛徒希望通过影响统一行动计划的制定与传播,破坏忠诚的将军们一致的行动计划。因此,将军们必须有一个预定的方法协议, 使所有忠诚的将军能够达成一致,而且少数几个叛徒不能使忠诚的将军做出错误的计划。也就是说,拜占庭将军问题的实质就是要寻找一个方法,使得将军们能在一 个有叛徒的非信任环境中建立对战斗计划的共识。在分布式系统中,特别是在区块链网络环境中,也和拜占庭将军的环境类似,有运行正常的服务器(类似忠诚的拜 占庭将军),有故障的服务器,还有破坏者的服务器(类似叛变的拜占庭将军)。共识算法的核心是在正常的节点间形成对网络状态的共识。
求解拜占庭将军问题,隐含要满足以下两个条件:
1)每个忠诚的将军必须收到相同的命令值vi(vi是第i个将军的命令)。
2)如果第i个将军是忠诚的,那么他发送的命令和每个忠诚将军收到的vi相同。
于是,拜占庭将军问题的可以描述为:一个发送命令的将军要发送一个命令给其余n-1个将军,使得:
IC1.所有忠诚的接收命令的将军遵守相同的命令;
IC2.如果发送命令的将军是忠诚的,那么所有忠诚的接收命令的将军遵守所接收的命令。
Lamport对拜占庭将军问题的研究表明[2] ,当n>3m时,即叛徒的个数m小于将军总数n的1/3时,通过口头同步通信(假设通信是可靠的),可以构造同时满足IC1和IC2的解决方案,即 将军们可以达成一致的命令。但如果通信是可认证、防篡改伪造的(如采用PKI认证,消息签名等),则在任意多的叛徒(至少得有两个忠诚将军)的情况下都可 以找到解决方案。
而在异步通信情况下,情况就没有这么乐观。Fischer-Lynch-Paterson定理证明了,只要有一个叛徒存在,拜占庭将军问题就无解[3] 。翻译成分布式计算语言,在一个多进程异步系统中,只要有一个进程不可靠,那么就不存在一个协议,此协议能保证有限时间内使所有进程达成一致。
由此可见,拜占庭将军问题在一个分布式系统中,是一个非常有挑战性的问题。因为分布式系统不能依靠同步通信,否则性能和效率将非常低。因此寻找一种实用的解决拜占庭将军问题的算法一直是分布式计算领域中的一个重要问题。
在这里,我们先给出分布式计算中有关拜占庭缺陷和故障的两个定义:
定义1: 拜占庭缺陷(Byzantine Fault):
任何观察者从不同角度看,表现出不同症状的缺陷。
定义2: 拜占庭故障(Byzantine Failure):
在需要共识的系统中由于拜占庭缺陷导致丧失系统服务。
在分布式系统中,不是所有的缺陷或故障都能称作拜占庭缺陷或故障。像死机、丢消息等缺陷或故障不能算为拜占庭缺陷或故障。拜占庭缺陷或故障是最严重缺陷或故障,拜占庭缺陷有不可预测、任意性的缺陷,例如遭黑客破坏,中木马的服务器就是一个拜占庭服务器。
在一个有拜占庭缺陷存在的分布式系统中,所有的进程都有一个初始值。在这种情况下,共识问题(Consensus Problem),就是要寻找一个算法和协议,使得该协议满足以下三个属性。
1)一致性(Agreement):所有的非缺陷进程都必须同意同一个值。
2)正确性(Validity):如果所有的非缺陷的进程有相同的初始值,那么所有非缺陷的进程所同意的值必须是同一个初始值。
3)可结束性(Termination):每个非缺陷的进程必须最终确定一个值。
根据Fischer-Lynch-Paterson的理论,在异步通信的分布式系统中,只要有一个拜占庭缺陷的进程, 就不可能找到一个共识算法,可同时满足上述要求的一致性、正确性和可结束性要求。在实际情况下,根据不同的假设条件,有很多不同的共识算法被设计出来。这 些算法各有优势和局限。算法的假设条件有以下几种情况:
1)故障模型:非拜占庭故障/拜占庭故障。
2)通信类型:同步/异步。
3)通信网络连接:节点间直连数。
4)信息发送者身份:实名/匿名。
5)通信通道稳定性:通道可靠/不可靠。
6)消息认证性:认证消息/非认证消息。
在区块链网络中,由于应用场景的不同,所设计的目标各异,不同的区块链系统采用了不同的共识算法。一般来说,在私有链 和联盟链情况下,对一致性、正确性有很强的要求。一般来说要采用强一致性的共识算法。而在公有链情况下,对一致性和正确性通常没法做到百分之百,通常采用 最终一致性(Eventual Consistency)的共识算法。
下面我们先来介绍适合私有链和联盟链场景的拜占庭容错系统。
[1] Lamport L,Shostak R,Pease M.The Byzantine generals problem.ACM Trans.on Programming Languages and Systems,1982,4(3):382-401.
[2] Lamport L,Shostak R,Pease M.The Byzantine generals problem.ACM Trans.on Programming Languages and Systems,1982,4(3):382-401.
[3] Fischer,M.J.,Lynch,N.A.,Paterson,M.:Impossibility of distributed consensus with one faulty process.J.ACM 32(2),374-382(1985).
5.1.2 拜占庭容错系统
上一节的分析表明,区块链网络的记账共识和拜占庭将军问题是相似的。参与共识记账的每一个记账节点相当于将军,节点之间的消息传递相当于信使,某些节点可能由于各种原因而产生错误的信息并传达给其他节点。通常,这些发生故障节点被称为拜占庭节点 ,而正常的节点即为非拜占庭节点 。
拜占庭容错系统是一个拥有n台节点的系统,整个系统对于每一个请求,满足以下条件:
1)所有非拜占庭节点使用相同的输入信息,产生同样的结果;
2)如果输入的信息正确,那么所有非拜占庭节点必须接收这个信息,并计算相应的结果。
与此同时,在拜占庭系统的实际运行过程中,还需要假设整个系统中拜占庭节点不超过m台,并且每个请求还需要满足两个指标。
·安全性:任何已经完成的请求都不会被更改,它可以在以后请求看到;
·活性:可以接受并且执行非拜占庭客户端的请求,不会被任何因素影响而导致非拜占庭客户端的请求不能执行。
拜占庭系统普遍采用的假设条件包括:
1)拜占庭节点的行为可以是任意的,拜占庭节点之间可以共谋;
2)节点之间的错误是不相关的;
3)节点之间通过异步网络连接,网络中的消息可能丢失、乱序并延时到达,但大部分协议假设消息在有限的时间里能传达到目的地;
4)服务器之间传递的信息,第三方可以嗅探到,但是不能篡改、伪造信息的内容和验证信息的完整性。
5.1.3 实用的拜占庭容错系统
原始的拜占庭容错系统[1] 由于需要展示其理论上的可行性而缺乏实用性。另外,还需要额外的时钟同步机制支持,算法的复杂度也是随节点增加而指数级增加。实用拜占庭容错系统(Practical Byzantine Fault Tolerance,PBFT)[2] ,降低了拜占庭协议的运行复杂度,从指数级别降低到多项式级别(Polynomial),使拜占庭协议在分布式系统中应用成为可能。
PBFT是一类状态机拜占庭系统[3] ,要求共同维护一个状态,所有节点采取的行动一致。为此,需要运行三类基本协议,包括一致性协议、检查点协议和视图更换协议。我们主要关注支持系统日常运行的一致性协议。
一致性协议要求来自客户端的请求在每个服务节点上都按照一个确定的顺序执行。这个协议把服务器节点分为两类:主节点和 从节点,其中主节点仅一个。在协议中,主节点负责将客户端的请求排序;从节点按照主节点提供的顺序执行请求。每个服务器节点在同样的配置信息下工作,该配 置信息被称为视图,主节点更换,视图也随之变化。
一致性协议至少包含若干个阶段:请求(request)、序号分配(pre-prepare)和响应(reply)。根据协议设计的不同,可能包含相互交互(prepare),序号确认(commit)等阶段。
PBFT的一致性协议如图5-1所示。PBFT系统通常假设故障节点数为m个,而整个服务节点数为3m+1个。每一个 客户端的请求需要经过5个阶段,通过采用两次两两交互的方式在服务器达成一致之后再执行客户端的请求。由于客户端不能从服务器端获得任何服务器运行状态的 信息,PBFT中主节点是否发生错误只能由服务器监测。如果服务器在一段时间内都不能完成客户端的请求,则会触发视图更换协议。
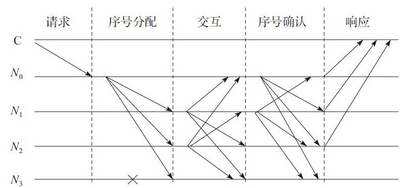
图5-1 PBFT协议通信模式
图5-1显示了一个简化的PBFT的协议通信模式,其中C为客户端,N0 ~N3 表示服务节点,特别的,N0 为主节点,N3 为故障节点。整个协议的基本过程如下。
1)客户端发送请求,激活主节点的服务操作。
2)当主节点接收请求后,启动三阶段的协议以向各从节点广播请求。
[2.1]序号分配阶段,主节点给请求赋值一个序列号n,广播序号分配消息和客户端的请求消息m,并将构造PRE-PREPARE消息给各从节点;
[2.2]交互阶段,从节点接收PRE-PREPARE消息,向其他服务节点广播PREPARE消息;
[2.3]序号确认阶段,各节点对视图内的请求和次序进行验证后,广播COMMIT消息,执行收到的客户端的请求并给客户端以响应。
3)客户端等待来自不同节点的响应,若有m+1个响应相同,则该响应即为运算的结果。
PBFT在很多场景都有应用,在区块链场景中,一般适合于对强一致性有要求的私有链和联盟链场景。例如,在IBM主导的区块链超级账本项目中,PBFT是一个可选的共识协议。
除了PBFT之外,超级账本项目还引入了基于PBFT的自用共识协议,它的目的是希望在PBFT基础之上能够对节点的 输出也做好共识,这是因为,超级账本项目的一个重要功能是提供区块链之上的智能合约,即在区块链上执行的一段代码,因此它会导致区块链账本上最终状态的不 确定,为此这个自有共识协议会在PBFT实现的基础之上,引入代码执行结果签名进行验证。
[1] Lamport L,Shostak R,Pease M.The Byzantine generals problem.ACM Trans.on Programming Languages and Systems,1982,4(3):382-401.
[2] Castro M,Liskov B.Practical Byzantine fault tolerance and proactive recovery.ACM Trans.on Computer Systems,2002,20(4):398-461.
[3] 范捷,易乐天,舒继武.拜占庭系统技术研究综述.软件学报,2013,24(6):1346-1360.
5.1.4 Raft协议
在很多分布式系统场景下,并不需要解决拜占庭将军问题,也就是说,在这些分布式系统的实用场景下,其假设条件不需要考 虑拜占庭故障,而只是处理一般的死机故障。在这种情况下,采用Paxos等协议会更加高效。Paxos是Lamport设计的保持分布式系统一致性的协 议。但由于Paxos非常复杂,比较难以理解,因此后来出现了各种不同的实现和变种。例如谷歌的GFS、BigTable就采用了基于Paxos的 Chubby的分布式锁协议;Yahoo的Hadoop系统采用了类似Paxos协议的Zookeeper协议。Raft也是为了避免Paxos的复杂性 而专门设计成易于理解的分布式一致性算法。在私有链和联盟链的场景下,通常共识算法有强一致性要求,同时对共识效率要求高。另外一般安全性要比公有链场景 高,一般来说不会经常存在拜占庭故障。因此,在一些场景下,可以考虑采用非拜占庭协议的分布式共识算法。
在Hyperledger的Fabric项目中,共识模块被设计成可插拔的模块,支持像PBFT、Raft等共识算法。
Raft最初是一个用于管理复制日志的共识算法[1] ,它是一个为真实世界应用建立的协议,主要注重协议的落地性和可理解性。Raft是在非拜占庭故障下达成共识的强一致协议。
在区块链系统中,使用Raft实现记账共识的过程可以描述如下:首先选举一个leader,接着赋予leader完全 的权力管理记账。leader从客户端接收记账请求,完成记账操作,生成区块,并复制到其他记账节点。有了leader简化了记账操作的管理。例 如,leader能够决定是否接受新的交易记录项而无需考虑其他的记账节点,leader可能失效或与其他节点失去联系,这时,系统就会选出新的 leader。
给定leader方法,Raft将共识问题分解为三个相对独立的子问题。
·leader选举:现有的leader失效时,必须选出新leader。
·记账:leader必须接受来自客户端的交易记录项,在参与共识记账的节点中进行复制,并使其他的记账节点认可交易所对应的区块。
·安全:若某个记账节点对其状态机应用了某个特定的区块项,其他的服务器不能对同一个区块索引应用不同的命令。
1.Raft基础
一个Raft集群通常包含5个服务器,允许系统有两个故障服务器。每个服务器处于3个状态之一:leader、 follower或candidate。正常操作状态下,仅有一个leader,其他的服务器均为follower。follower是被动的,不会对自 身发出请求而是对来自leader和candidate的请求做出响应。leader处理所有的客户端请求(若客户端联系follower,则该 follower将转发给leader)。candidate状态用来选举leader。
Raft阶段主要分为两个,首先是leader选举过程,然后在选举出来的leader基础上进行正常操作,比如日志复制、记账等。
2.leader选举
当follower在选举超时时间内未收到leader的心跳消息,则转换为candidate状态。为了避免选举冲突,这个超时时间是一个150~300ms之间的随机数。
一般而言,在Raft系统中:
1)任何一个服务器都可以成为一个候选者candidate,它向其他服务器follower发出要求选举自己的请求。
2)其他服务器同意了,发出OK。注意,如果在这个过程中,有一个follower宕机,没有收到请求选举的要求,此时候选者可以自己选自己,只要达到N/2+1的大多数票,候选人还是可以成为leader的。
3)这样这个候选者就成为了leader领导人,它可以向选民也就是follower发出指令,比如进行记账。
4)以后通过心跳进行记账的通知。
5)一旦这个leader崩溃了,那么follower中有一个成为候选者,并发出邀票选举。
6)follower同意后,其成为leader,继续承担记账等指导工作。
3.记账过程
Raft的记账过程按以下步骤完成:
1)假设leader领导人已经选出,这时客户端发出增加一个日志的要求;
2)leader要求follower遵从他的指令,都将这个新的日志内容追加到他们各自日志中;
3)大多数follower服务器将交易记录写入账本后,确认追加成功,发出确认成功信息;
4)在下一个心跳中,leader会通知所有follower更新确认的项目。
对于每个新的交易记录,重复上述过程。
如果在这一过程中,发生了网络通信故障,使得leader不能访问大多数follower了,那么leader只能正 常更新它能访问的那些follower服务器。而大多数的服务器follower因为没有了leader,他们将重新选举一个候选者作为leader,然 后这个leader作为代表与外界打交道,如果外界要求其添加新的交易记录,这个新的leader就按上述步骤通知大多数follower,如果这时网络 故障修复了,那么原先的leader就变成follower,在失联阶段,这个老leader的任何更新都不能算确认,都回滚,接收新的leader的新 的更新。
本节介绍了分布式系统中的常用共识算法。从介绍拜占庭将军问题开始,介绍了拜占庭容错系统、状态机拜占庭协议、实用拜占庭容错协议(PBFT)和Raft。其中拜占庭容错协议和Raft是联盟链和私有链上常用的共识算法。
而公共链的共识机制一般采用工作量证明(POW)和权益证明(POS)算法。下面进行介绍。
[1] Ongaro D,Ousterhout J.In Search of an Understandable Consensus Algorithm.In:Proc.of USENIX Annual Technical Conference 2014,305-319.
来源:我是码农,转载请保留出处和链接!
本文链接:http://www.54manong.com/?id=1020
微信号:qq444848023 QQ号:444848023
加入【我是码农】QQ群:864689844(加群验证:我是码农)
- 3.15 存在、真实性和所有权合约的证明2018-09-15 23:34
- 第10章 区块链应用案例分析2018-09-30 14:06
- 未来: 从Uber到Suber2018-09-04 22:55
- 区块链在认证领域的应用案例2018-09-21 10:20
网站分类
- 数据结构
- 数据结构视频教程
- 数据结构练习题
- 数据结构试卷
- 数据结构习题解析
- 数据结构电子书
- 数据结构精品文章
- 区块链
- 区块链精品文章
- 区块链电子书
- 大数据
- 大数据精品文章
- 大数据电子书
- 机器学习
- 机器学习精品文章
- 机器学习电子书
- 面试笔试
- 物联网/云计算
标签列表
- 数据结构 (39)
- 数据结构电子书 (20)
- 数据结构习题解析 (8)
- 数据结构试卷 (10)
- 区块链是什么 (261)
- 数据结构视频教程 (31)
- 大数据技术与应用 (12)
- 百面机器学习 (14)
- 机器学电子书 (29)
- 大数据电子书 (37)
- 程序员面试 (10)
- RFID (21)
最近发表
- 找出数组中有3个出现一次的数字
- 《百面机器学习》电子书下载
- 区块链精品电子书《深度探索区块链:Hyperledger技术与应用_区块链技术丛书》张增骏
- 区块链精品电子书《比特币:一个虚幻而真实的金融世界》
- 区块链精品电子书《图说区块链》-徐明星 & 田颖 & 李霁月
- 区块链精品电子书《是非区块链:技术、投机与泡沫》-英国《金融时报》
- 区块链精品电子书《商业区块链:开启加密经济新时代》-威廉·穆贾雅
- 区块链精品电子书《人工智能时代,一本书读懂区块链金融 (互联网_时代企业管理实战系列)》-马兆林
-
(function(){
var bp = document.createElement('script');
var curProtocol = window.location.protocol.split(':')[0];
if (curProtocol === 'https'){
bp.src = 'https://zz.bdstatic.com/linksubmit/push.js';
}
else{
bp.src = 'http://push.zhanzhang.baidu.com/push.js';
}
var s = document.getElementsByTagName("script")[0];
s.parentNode.insertBefore(bp, s);
})();
全站首页 | 数据结构 | 区块链| 大数据 | 机器学习 | 物联网和云计算 | 面试笔试
var cnzz_protocol = (("https:" == document.location.protocol) ? "https://" : "http://");document.write(unescape("%3Cspan id='cnzz_stat_icon_1276413723'%3E%3C/span%3E%3Cscript src='" + cnzz_protocol + "s23.cnzz.com/z_stat.php%3Fid%3D1276413723%26show%3Dpic1' type='text/javascript'%3E%3C/script%3E"));本站资源大部分来自互联网,版权归原作者所有!






评论专区