公钥密码算法是现代密码学发展过程中的一个里程碑。这类密码算法需要两个密钥：公开密钥和私有密钥。公开密钥与私有密 钥是一对，如果用公开密钥对数据进行加密，只有用对应的私有密钥才能解密；如果用私有密钥对数据进行加密，那么只有用对应的公开密钥才能解密。因为加密和 解密使用的是两个不同的密钥，所以这种算法也可叫作非对称密码算法。

区块链中所使用的公钥密码算法是椭圆曲线算法，每个用户都拥有一对密钥，一个公开，另一个私有。利用椭圆曲线密码算 法，用户可以用自己的私钥对交易信息进行签名，同时别的用户可以利用签名用户的公钥对签名进行验证。在比特币系统中，用户的公钥也被用来识别不同的用户， 构造用户的比特币地址。下面我们将介绍区块链中所涉及的椭圆曲线算法以及所采用的椭圆曲线。

4.3.1　椭圆曲线密码算法

椭圆曲线密码（Elliptic Curve Cryptography，ECC）算法是基于椭圆曲线数学的一种公钥密码的算法，其安全性依赖于椭圆曲线离散对数问题的困难性。

椭圆曲线密码算法具有下面两个明显的优点：

1）短的密钥长度，这意味着小的带宽和存储要求；

2）所有的用户可以选择同一基域上的不同的椭圆曲线，可使所有的用户使用同样的操作完成域运算。

椭圆曲线可以定义如下：

设p是一个大于3的素数，在有限域Fp上的椭圆曲线y2 =x3 +ax+b由一个基于同余式y2 =x3 +ax+b mod p的解集（x，y）∈Fp ×Fp 和一个称为无穷远点的特定点O组成，这里a，b∈Fp是两个满足4a3 +27b2 ≠0mod p的常数。

图4-5显示了两种实际的椭圆曲线。

图4-5　椭圆曲线

设P1 =（x1 ，y1 ）与P2 =（x2 ，y2 ）为椭圆曲线上的两个点，我们可以定义椭圆曲线上的加法和减法运算如下：

1）-O=O

2）-P1 =（x1 ，-y1 ）

3）O+P1 =P1

4）若P2 =-P2 ，则P1 +P2 =O

5）若P2 ≠-P1 ，则P1 +P2 =（x3 ，y3 ），其中x3 =m2 -x1 -x2 ，-y3 =m（x3 -x1 ）+y1 ，

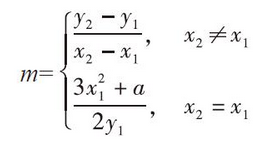
依据上述定义的加减法，两个椭圆曲线上的点相加所得到的点依然在原椭圆曲线上。图4-6直观地解释了椭圆曲线上的两个点P与Q相加的结果。

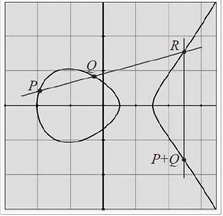
图4-6　椭圆曲线上的两个点相加

由此，在等式kP=P+P+…+P=Q中，已知k和点P，求点Q比较容易，反之已知点Q和点P，求k却是相当困难的，这个问题称为椭圆曲线上点群的离散对数问题。椭圆曲线密码体制正是利用这个困难问题设计的。在实际应用中，k作为私有密钥，而Q作为公开密钥。

4.3.2　secp256k1椭圆曲线

比特币系统的区块链实现中使用的椭圆曲线为Certicom推荐的椭圆曲线secp256k1。

Certicom是国际上著名的椭圆曲线密码技术公司，已授权300多家企业使用ECC密码技术，secp256k1为基于Fp 有限域上的椭圆曲线，由于其构造的特殊性，其优化后的实现比其他曲线性能上可以提高30%，对比NIST推荐的曲线，secp256k1的常数以可以预测的方法选择，可以有效避免后门出现的可能性。

secp256k1曲线形如y2 =x3 +ax+b，由六元组D=（p，a，b，G，n，h）定义，其中：

压缩形式表示的基点G为：

G=02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D959F2815B 16F81798

而非压缩形式的表示为：

G=04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

G的阶为：

n=FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

协因子为：

h=01

4.3.3　椭圆曲线签名与验证签名

我们先简单描述一下椭圆曲线的签名与验证算法。

（1）椭圆曲线数字签名生成

假定Alice希望对消息m进行签名，她所采用的椭圆曲线参数为D=（p，a，b，G，n，h）（见上节中各参数定义），对应的密钥对为（k，Q），其中Q为公钥，k为私钥。Alice将按如下步骤进行签名。

第1步，产生一个随机数d，1≤d≤n-1；

第2步，计算dG=（x1 ，y1 ），将x1 转化为整数x1 ；

第3步，计算r=x1 mod n，若r=0，则转向第1步；

第4步，计算d-1 mod n；

第5步，计算哈希值H（m），并将得到的比特串转化为整数e；

第6步，计算s=d-1 （e+kr）mod n，若s=0，则转向第一步；

第7步，（r，s）即为Alice对消息m的签名。

（2）椭圆曲线签名验证

为验证Alice对消息m的签名（r，s），矿工（Miner）可以得到Alice所用的椭圆曲线参数以及Alice的公钥Q。矿工将按以下步骤操作。

第1步，验证r和s是区间[1，n-1]上的整数；

第2步，计算H（m）并将其转化为整数e；

第3步，计算w=s-1 mod n；

第4步，计算u1 =ew mod n以及u2 =rw mod n；

第5步，计算X=u1 G+u2 Q；

第6步，若X=O，则拒绝签名，否则将X的x坐标x1 转化为整数x1 ，并计算v=x1 mod n；

第7步，当且仅当v=r时，签名通过验证。

为具体说明椭圆曲线签名和验证算法的过程，我们来看一个简化的例子：Alice决定把10个比特币支付给Bob，矿工负责把这笔账给记录下来。这个过程是怎么使用签名和验证算法进行的呢？

首先Alice从自己钱包中取出10个比特币，要将这10个比特币支付给Bob，于是交易消息m产生了：Alice支 付10BTC给Bob。由于这个消息需要向全网广播，收到这个交易消息的用户会发生疑问：这个交易是不是真的？为打消其他用户的疑虑，Alice需要对这 段交易消息进行数字签名，以向大家确定这个交易确实是Alice发出的。为此，Alice使用了secp256k1椭圆曲线。签名本质上是对交易消息内容 进行使用Alice的私钥k加密（签名算法的第6步）。考虑到消息的规模和公钥密码算法的效率，对交易消息进行的签名实际上是对交易消息的哈希值进行签 名，由于密码哈希函数的抗碰撞性，可以认为这样的转化是合理有效的。于是Alice向全网广播的内容除了交易消息本身外，还包含Alice对消息的签名以 及Alice的公钥信息。

其次，Alice发送的交易消息连同签名发出后，为矿工Miner所接收。为在区块链中记录这一交易，矿工首先需要验 证这个交易是不是Alice发出的，即进行签名验证的工作。为此，Miner也使用了同样的secp256k1椭圆曲线。对Alice签名验证的过程可以 看作利用Alice公钥进行解密的过程，如签名验证算法中的第5步就使用了Alice的公钥Q。当一切顺利的话，Miner可以验证交易消息：Alice 支付10BTC给Bob确实是Alice发出的，Miner可以在之后的操作中把这个交易记入区块链中。如果签名验证失败，表明Miner收到的这个消息 存在问题，Miner会放弃将相关的交易记入区块链的操作。

利用椭圆曲线的签名和验证算法，一方面可以保证用户的账户不被冒名顶替，另一方面也能确保用户不能否认其所签名的交 易。用户发起交易的时候，使用自己的私钥对交易信息签名，矿工收到信息后用用户的公钥对签名进行验证，一旦通过，该交易信息就可通过矿工进行记账，最终完 成交易。

本章简介了区块链中的密码技术。区块链通常并不直接保存原始数据或交易记录，而是保存其哈希函数值，更具体的，比特币 区块链通常采用双SHA256哈希函数，即将任意长度的原始数据经过两次SHA256哈希运算后转换为长度为256位（32字节）的二进制数字来统一存储 和识别。为快速归纳和校验区块数据的存在性和完整性，Merkle树成为区块链的重要数据结构。公钥密码系统被用来实现区块链中的数据签名，比特币区块链 中采用了椭圆曲线公钥密码系统，使用了Certicom推荐的secp256k1椭圆曲线。

参考资料

［1］Arvind Narayanan，Joseph Bonneau，Edward Felten，Andrew Miller，Steven Goldfeder.Bitcoin and Cryptocurrency Technologies.Princeton University Press，2016.

［2］（加）Douglas R.Stinson.密码学原理与实践（第3版）电子工业出版社2009.

［3］https://en.wikipedia.org/wiki/SHA-3 .

［4］https://en.wikipedia.org/wiki/Scrypt.

来源：我是码农，转载请保留出处和链接！

本文链接：http://www.54manong.com/?id=1022

• 二、支付汇款2018-09-25 15:17
• 4.9　知识点导图2018-08-25 17:18
• 罪犯们也会使用这个网络2018-09-04 22:32
• 10.6 侧链——基于比特币的另类币2018-09-12 10:58