注意:这是我遗留下来的非常老的教程,但是我不认为应该参考或使用它。更好的材料包括CS231n课程的讲座,幻灯片和笔记,或《深度学习》书。
嗨,我是斯坦福大学的CS博士学位学生。作为研究的一部分,我从事深度学习已经有几年了,与我相关的几个宠物项目中有一个是ConvNetJS-一个用于训练神经网络的Javascript库。Javascript使人们可以很好地可视化正在发生的事情,并可以使用各种超参数设置进行操作,但是我仍然经常听到有人要求对该主题进行更彻底的处理。这篇文章(我打算慢慢扩展到几本书的章节)是我的谦虚尝试。它在网络上而不是PDF上,因为所有书籍都应该在这本书上,最终它有望包括动画/演示等。
我在神经网络方面的亲身经历是,当我开始忽略反向传播方程的整页密集稠密推导并开始编写代码时,一切都变得更加清晰。因此,本教程将只包含很少的数学运算(我不认为这是必要的,有时甚至会混淆简单的概念)。因为我的背景是计算机科学和物理,所以我将改用我所说的黑客的观点来发展这个主题。我的论述将围绕代码和物理直觉而不是数学推导。基本上,我将以一种希望刚开始时遇到的方式来介绍算法。
“……当我开始编写代码时,一切都变得更加清晰。”
您可能会急切地想要学习神经网络,反向传播,如何将它们实际应用到数据集等。但是在到达那里之前,我希望我们首先忘记所有这些。让我们退后一步,了解核心的实际情况。首先让我们谈谈实值电路。
更新说明:不久前,我暂停了本指南的工作,并将精力投入到斯坦福大学的CS231n(卷积神经网络)课程上。注释位于cs231.github.io上,可以在此处找到课程幻灯片。这些材料与此处的材料高度相关,但功能更全面,有时更精致。
第一章:实值电路
以我的观点,认为神经网络的最佳方法是使用实值电路,其中实值(而不是布尔值{0,1})沿着边缘“流动”并在门中相互作用。然而,代替门如AND,OR,NOT,等,我们有二门,例如*(乘), +(加),max或一元门如exp等不同于普通的布尔电路,但是,我们最终也将有梯度的流动电路的相同边缘,但方向相反。但是,我们正在超越自我。让我们集中精力,从简单开始。
基本案例:电路中的单门
首先让我们考虑一个带有一个门的简单电路。这是一个例子:
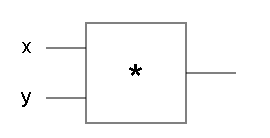
该电路采用两个实值输入x,y并x * y通过*门进行计算。这样的Javascript版本看起来非常简单:
var forwardMultiplyGate = function(x, y) {
return x * y;};forwardMultiplyGate(-2, 3); // returns -6. Exciting.而在数学形式中,我们可以将此门视为实现实值函数:
F(x ,y)= x yF(x ,y)= x yF(x ,y)= x yF(x ,y)= x yF(x ,y)= x yF(x ,y)== x y
与本示例一样,我们所有的门都将接受一个或两个输入并产生单个输出值。
目标
我们感兴趣的问题如下所示:
我们提供一个给定的电路部分特定的输入值(例如
x = -2,y = 3)电路计算输出值(例如
-6)核心问题变成:如何稍微调整输入以增加输出?
在这种情况下,我们应该朝哪个方向改变x,y以获得大于的数字-6?请注意,例如,x = -1.99和y = 2.99给出x * y = -5.95,该值高于-6.0。不要为此感到困惑:-5.95比更好(更高)-6.0。这是一个进步0.05,尽管幅度的-5.95(一般为从零距离)恰好是较低的。
策略1:随机本地搜索
好的。那么等等,我们有一个电路,我们有一些输入,我们只想稍微调整一下它们以增加输出值?为什么这很难?我们可以轻松地“转发”电路以计算给定x和的输出y。那么这不重要吗?我们为什么不随机进行调整x并y跟踪最有效的调整:
// circuit with single gate for nowvar forwardMultiplyGate = function(x, y) { return x * y; };var x = -2, y = 3; // some input values// try changing x,y randomly small amounts and keep track of what works bestvar tweak_amount = 0.01;var best_out = -Infinity;var best_x = x, best_y = y;for(var k = 0; k < 100; k++) {
var x_try = x + tweak_amount * (Math.random() * 2 - 1); // tweak x a bit
var y_try = y + tweak_amount * (Math.random() * 2 - 1); // tweak y a bit
var out = forwardMultiplyGate(x_try, y_try);
if(out > best_out) {
// best improvement yet! Keep track of the x and y
best_out = out;
best_x = x_try, best_y = y_try;
}}当我跑,我得到best_x = -1.9928,best_y = 2.9901和best_out = -5.9588。再次-5.9588高于-6.0。所以,我们完成了,对吧?不完全是:如果您有足够的计算时间,对于只有几个门的小问题,这是一种非常好的策略,但是如果我们最终要考虑具有数百万个输入的大型电路,那么它就不会起作用。事实证明,我们可以做得更好。
策略2:数值梯度
这是一个更好的方法。再次记住,在我们的设置中,我们得到了一个电路(例如,我们的单*门电路)和一些特定的输入(例如x = -2, y = 3)。门计算输出(-6),现在我们要调整x并y提高输出。
关于我们要做的事情的一个很好的直觉如下:想象一下从电路中获得的输出值并向正方向拉动它。这种正张力将依次通过闸门平移并在输入端x和输入端上产生力y。告诉我们如何x以及y应该如何改变以增加输出值的力量。
在我们的特定示例中,这些力量可能是什么样的?仔细考虑一下,我们可以直觉施加的力x也应为正,因为x稍大一点可以改善电路的输出。例如,x从x = -2增加到x = -1将使我们的输出-3-比更大-6。另一方面,我们希望在其上产生负作用力y,使它变低(因为从原始值开始降低y,例如y = 2,将降低y = 3输出2 x -2 = -4,使输出更高,再次大于-6)。无论如何,这是要记住的直觉。当我们经历这个过程时,事实证明,我所描述的力实际上将是派生的输出值相对于其输入(x和y)的关系。您可能以前曾听过这个词。
当我们拉动输出变得更高时,可以将导数视为对每个输入的作用力。
那么,我们如何准确地评估这个力(导数)呢?事实证明,有一个非常简单的过程。我们将向后工作:我们不会逐个循环输入,而是逐个迭代每个输入,将其略微增加,然后观察输出值会发生什么。输出响应的变化量为导数。现在有足够的直觉。让我们看一下数学定义。我们可以针对输入写下函数的导数。例如,关于的导数x可以计算为:
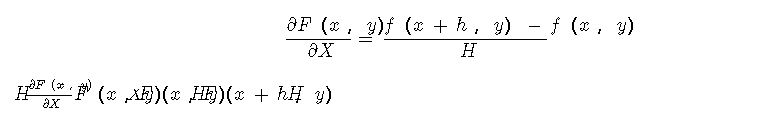
var x = -2, y = 3;var out = forwardMultiplyGate(x, y); // -6var h = 0.0001;// compute derivative with respect to xvar xph = x + h; // -1.9999var out2 = forwardMultiplyGate(xph, y); // -5.9997var x_derivative = (out2 - out) / h; // 3.0// compute derivative with respect to yvar yph = y + h; // 3.0001var out3 = forwardMultiplyGate(x, yph); // -6.0002var y_derivative = (out3 - out) / h; // -2.0
让我们x来举例说明。我们从原来的旋钮x来x + h和电路回应给予更高的值(再次指出,是的,-5.9997是更高的比-6:-5.9997 > -6)。除以此处的h值是根据h我们在此处选择的(任意)值对电路的响应进行归一化。从技术上讲,您希望的值h是无穷小的(将梯度的精确数学定义定义为表达式的极限,h然后变为零),但实际上h=0.00001,在大多数情况下都能很好地获得良好的近似值。现在,我们看到导数wrt x为+3。我要明确表示正号,因为它表示电路正在拉扯x以使其变高。实际值3可以解释为该拖船的力。
通过微调该输入并观察输出值的变化,可以计算出某些输入的导数。
顺便说一句,我们通常谈论关于单个输入的导数,或者关于所有输入的梯度。梯度仅由向量(即列表)中串联的所有输入的导数组成。至关重要的是,请注意,如果让输入通过跟随梯度很小的量来响应拖轮(即,我们仅将导数添加到每个输入的顶部),就可以看到值按预期增加了:
var step_size = 0.01;var out = forwardMultiplyGate(x, y); // before: -6x = x + step_size * x_derivative; // x becomes -1.97y = y + step_size * y_derivative; // y becomes 2.98var out_new = forwardMultiplyGate(x, y); // -5.87! exciting.
正如预期的那样,我们通过梯度更改了输入,现在电路给出的值稍高(-5.87 > -6.0)。这比尝试对x和随机更改要简单得多y,对吗?这里值得欣赏的事实是,如果进行微积分,则可以证明梯度实际上是函数最陡峭的增长方向。无需像策略1中那样随意尝试随机插管。评估梯度只需要对电路的正向通过三个评估,而不是数百次,并且如果您有兴趣增加输出值,则可以提供(本地)最好的拖船。
迈出更大的一步并不总是更好。让我在这一点上澄清一下。重要的是要注意,在这个非常简单的示例中,使用step_size大于0.01的值始终会更好。例如,step_size = 1.0给出输出-1(更高更好!),实际上无限步长将产生无限好的结果。要意识到的关键是,一旦我们的电路变得更加复杂(例如整个神经网络),从输入到输出值的功能就会更加混乱和摇摆。渐变保证了,如果步长非常小(实际上是无限小),那么按照步长方向一定会得到一个更大的数字,对于步长无限小,没有其他方向会更好。但是,如果您使用更大的步长(例如step_size = 0.01)所有投注均关闭。之所以能以比无限小的步长更大的步长逃脱,是因为我们的函数通常相对平滑。但是,实际上,我们正在竭尽全力,希望能取得最好的成绩。
爬山类比。我以前听过一个比喻,我们的电路的输出值就像小山的高度,我们蒙住了双眼,试图向上爬。我们可以感觉到脚下山坡的陡峭程度(坡度),因此当我们稍微洗脚时,我们会往上走。但是,如果我们迈出了大步,过度自信的一步,那我们本来可以步入一个陷阱。
太好了,我希望我已经说服了您,数值梯度的确是非常有用的评估,而且价格便宜。但。事实证明,我们可以做的,甚至更好。
策略#3:分析梯度
在上一节中,我们通过探测电路的输出值来独立于每个输入来评估梯度。此过程将为您提供所谓的数值梯度。但是,这种方法仍然很昂贵,因为当我们独立地微调每个输入值时,我们需要计算电路的输出。因此,评估梯度的复杂度在输入数量上是线性的。但是实际上,我们将有成千上万个(对于神经网络而言)甚至数以千万计的输入,并且电路不仅是一个乘法门,而且还有庞大的表达式,这些表达式的计算成本很高。我们需要更好的东西。
幸运的是,有一种更简单,更快速的方法来计算梯度:我们可以使用微积分为其导出直接表达式,该表达式的计算与电路输出值一样简单。我们称其为解析梯度,无需进行任何调整。您可能已经看到其他教过神经网络的人通过巨大的坦率的,令人恐惧的和令人困惑的数学方程式(如果您不精通数学的话)推导梯度。但这是不必要的。我已经编写了很多神经网络代码,几乎不需要做超过两行的数学推导,而且95%的时间可以完全不用编写任何东西。那是因为我们将永远只导出非常小的和简单的表达式的梯度(认为它是基本情况)),然后向您展示如何使用链式规则非常简单地将它们组合起来以评估整个梯度(考虑归纳/递归的情况)。
解析导数不需要调整输入。可以使用数学(微积分)导出。
如果您还记得产品规则,幂规则,商规则等(例如,请参见派生规则或Wiki页面),则可以很容易地针对两者x以及y诸如这样的小表达式写下派生词x * y。但是,假设您不记得演算规则。我们可以回到定义。例如,这是派生wrt的表达式x:
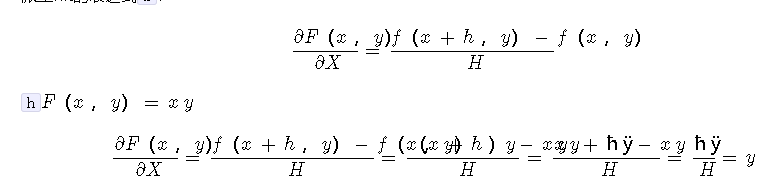
那很有意思。的导数x等于y。您是否注意到上一节中的巧合?我们调整了x对x+h和计算x_derivative = 3.0,这正是恰好是价值y的那个例子。事实证明,这根本不是巧合,因为那正是解析梯度告诉我们该x导数应为的原因f(x,y) = x * y。y顺便说一下,关于x对称的导数竟然是。因此,无需任何调整!我们调用了强大的数学,现在可以将导数计算转换为以下代码:
var x = -2, y = 3;var out = forwardMultiplyGate(x, y); // before: -6var x_gradient = y; // by our complex mathematical derivation abovevar y_gradient = x;var step_size = 0.01;x += step_size * x_gradient; // -1.97y += step_size * y_gradient; // 2.98var out_new = forwardMultiplyGate(x, y); // -5.87. Higher output! Nice.
为了计算梯度,我们从转发电路数百次(策略1)到仅按输入数量两倍(策略2)的数量级转发电路,再到转发一次!而且它变得更好,因为更昂贵的策略(#1和#2)仅给出了梯度的近似值,而#3(迄今为止最快的策略)为您提供了精确的梯度。没有近似值。唯一的缺点是您应该熟悉一些微积分101。
让我们回顾一下我们学到的东西:
输入:给我们一个电路,一些输入并计算一个输出值。
输出:然后,我们有兴趣发现(独立地)对每个输入进行小的更改,这些更改会使输出更高。
策略1:一种愚蠢的方法是随机搜索输入的小插值,并跟踪导致最大输出增加的原因。
策略2:我们发现通过计算梯度可以做得更好。无论电路多么复杂,数值梯度的计算都非常简单(但相对昂贵)。我们通过一次调整一个输入来探测电路的输出值来计算它。
策略#3:最后,我们看到我们可以更加聪明,并通过分析得出一个直接表达式来获得解析梯度。它与数值梯度相同,是目前为止最快的,不需要任何调整。
顺便说一句,在实践中(稍后我们将再次介绍),所有神经网络库始终会计算解析梯度,但通过将其与数值梯度进行比较可以验证实现的正确性。这是因为数值梯度很容易估算(但计算起来可能会有点昂贵),而解析梯度有时会包含错误,但通常计算效率非常高。正如我们将看到的,评估梯度(即在进行反向传播或向后通过时)的成本大约等于评估向前通过的成本。
递归情况:具有多个门的电路
但是请继续说:“对于您的超简单表达式,解析梯度微不足道。这没用。表达式大得多怎么办?方程式不是很快变得庞大而复杂吗?”。好问题。是的,表达式变得更加复杂。不,这并不会增加难度。就像我们将看到的那样,每个门都将自己挂出,完全不知道它可能包含的庞大而复杂的电路的任何细节。它将仅担心其输入,并且将如上一节所述计算其本地导数,除非现在将要做一次额外的乘法。
单个额外的乘法会将单个(无用的门)变成复杂的机器(整个神经网络)中的齿轮。
我现在应该停止大肆宣传。希望我引起了您的兴趣!让我们深入研究细节,并在下一个示例中涉及两个方面:
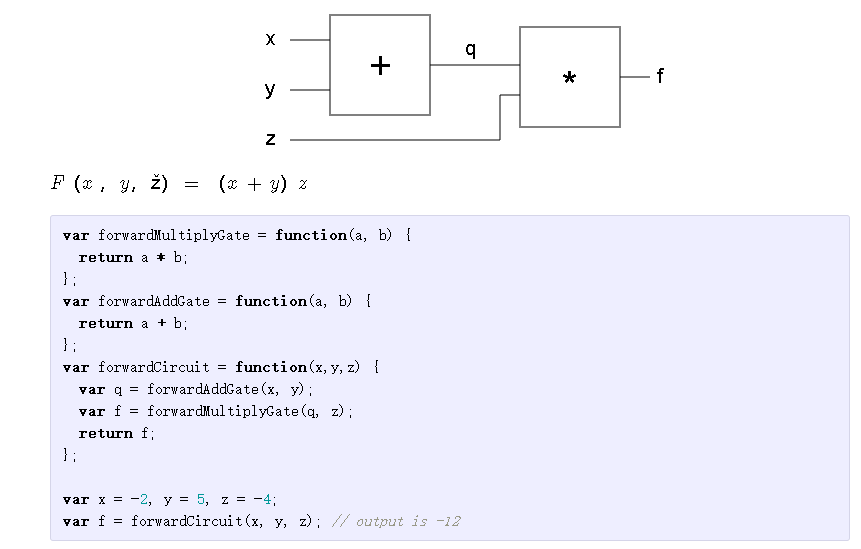
在上面,我在门函数中使用a和b作为局部变量,这样我们就不会将它们与电路输入相混淆x,y,z。和以前一样,我们有兴趣针对三个输入找到导数x,y,z。但是,既然涉及多个门,我们如何计算呢?首先,让我们假设+门不存在,并且电路中只有两个变量:q,z一个*门。注意,qis是+门的输出。如果我们不担心x和y而是只关心q和z,那么我们将回到只有一个门,直到那个门*关于门,我们知道上一节中的(解析)派生词是什么。我们可以把它们写下来(除了在这里我们要替换x,y用q,z):

那里有很多符号,所以也许这再次令人困惑,但是实际上只是两个数字相乘。这是代码:
// initial conditionsvar x = -2, y = 5, z = -4;var q = forwardAddGate(x, y); // q is 3var f = forwardMultiplyGate(q, z); // output is -12// gradient of the MULTIPLY gate with respect to its inputs// wrt is short for "with respect to"var derivative_f_wrt_z = q; // 3var derivative_f_wrt_q = z; // -4// derivative of the ADD gate with respect to its inputsvar derivative_q_wrt_x = 1.0;var derivative_q_wrt_y = 1.0;// chain rulevar derivative_f_wrt_x = derivative_q_wrt_x * derivative_f_wrt_q; // -4var derivative_f_wrt_y = derivative_q_wrt_y * derivative_f_wrt_q; // -4
而已。我们计算了梯度(力),现在我们可以让输入稍微响应它。让我们在输入上方添加渐变。电路的输出值最好从-12增加!
// final gradient, from above: [-4, -4, 3]var gradient_f_wrt_xyz = [derivative_f_wrt_x, derivative_f_wrt_y, derivative_f_wrt_z]// let the inputs respond to the force/tug:var step_size = 0.01;x = x + step_size * derivative_f_wrt_x; // -2.04y = y + step_size * derivative_f_wrt_y; // 4.96z = z + step_size * derivative_f_wrt_z; // -3.97// Our circuit now better give higher output:var q = forwardAddGate(x, y); // q becomes 2.92var f = forwardMultiplyGate(q, z); // output is -11.59, up from -12! Nice!
看起来很有效!现在让我们尝试直观地解释刚刚发生的事情。该电路希望输出更高的值。最后的闸门看到了输入q = 3, z = -4和计算出的输出-12。“拉”向上上诱导的两个力该输出值q和z:为了增加输出值,电路“要” z增加,因为可以通过衍生物(的正值可以看出derivative_f_wrt_z = +3)。同样,该导数的大小可以解释为力的大小。在另一方面,q感觉更强,向下的力,因为derivative_f_wrt_q = -4。换句话说,电路要q以的力减小4。
现在我们进入第二个+门,输出q。默认情况下,+门计算及其衍生物,它告诉我们如何改变x和y作出q更高。但!这里是关键的一点:在梯度q被计算为负(derivative_f_wrt_q = -4),所以电路要q以降低,并与力4!因此,如果+门想为增大最终输出值做出贡献,则需要监听来自顶部的梯度信号。在这种特殊情况下,它需要在x,y与通常使用的相反的方向上应用拖船4,可以说,力为。乘以-4在链式法则看出实现正是这种:而不是施加的正力+1在两个x和y上(本地衍生物),全电路的梯度都x和y变1 x -4 = -4。这是有道理的:电路希望双方x并y变得更小,因为这将使q小,这反过来又会使f较大。
如果这有道理,则可以理解反向传播。
让我们再次回顾一下我们学到的东西:
在上一章中,我们看到了在单个门(或单个表达式)的情况下,我们可以使用简单的演算来得出解析梯度。我们将梯度解释为一种力,或者说是对输入的拉力,将其拉向某个方向,该方向会使该门的输出更高。
在有多个门的情况下,一切都几乎保持相同的方式:每个门自身都在闲逛,完全不知道其所嵌入的电路。一些输入进来,并且门计算其输出以及相对于输入的导数。现在唯一的区别是突然之间,有些东西可以从上方拉到这扇门上。这是最终电路输出值相对于此门计算出的输出的梯度。该电路要求门以一定的力输出更高或更低的数字。闸门简单地吸收此力并将其乘以之前为其输入计算的所有力(链式规则)。这具有预期的效果:
如果闸门从上方受到强大的正向拉力,则其自身的输入也会受到更大拉力,这取决于闸门从上方受到的力
而且,如果它经历负向拉力,则意味着电路希望其值减小而不增加,因此它将翻转其输入上的拉力以减小其自身的输出值。
要记住的一幅好图是,当我们在最后拉电路的输出值时,这会导致整个电路向下下拉,一直到输入。
不漂亮吗 单门和计算任意复杂表达式的多个交互门之间的唯一区别是,此附加乘积运算现在在每个门中进行。
“向后”流程中的模式
让我们再次看一下示例电路,其中填充了数字。第一个电路显示原始值,第二个电路显示返回到输入的梯度,如前所述。请注意,渐变总是从+1结尾开始,以开始创建链。这是(默认)拉动电路以增加其值。
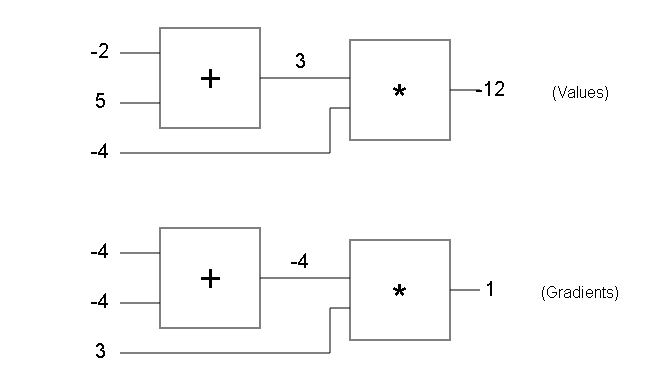
一段时间后,您开始注意到梯度在电路中如何反向流动的模式。例如,+门总是将梯度放在顶部,然后将其简单地传递到其所有输入(请注意,将-4的示例简单地传递到+门的两个输入)。这是因为+1,不管输入的实际值是多少,输入本身的导数都是just ,因此在链式规则中,上方的梯度仅乘以1并保持不变。类似的直觉适用于例如max(x,y)门。由于max(x,y)相对于其输入的梯度是+1的任意一个x,y因此较大,并且0 另一方面,此门实际上是在反向传播期间仅是一个梯度“开关”:它将从上方获取梯度并将其“路由”到前向通过期间具有较高值的输入。
数值梯度检查。在完成本节之前,仅需确保上面通过反向传播计算出的(解析)梯度正确无误即可。请记住,我们可以简单地通过计算数值梯度,并确保我们得到这样做[-4, -4, 3]的x,y,z。这是代码:
// initial conditionsvar x = -2, y = 5, z = -4;// numerical gradient checkvar h = 0.0001;var x_derivative = (forwardCircuit(x+h,y,z) - forwardCircuit(x,y,z)) / h; // -4var y_derivative = (forwardCircuit(x,y+h,z) - forwardCircuit(x,y,z)) / h; // -4var z_derivative = (forwardCircuit(x,y,z+h) - forwardCircuit(x,y,z)) / h; // 3
然后我们得到[-4, -4, 3],是使用backprop计算得出的。唷!:)
示例:单神经元
希望在上一节中了解了反向传播的基本知识。现在,让我们来看一个更复杂和临界的实际示例。我们将考虑一个二维神经元,它计算以下功能:

例如,如果S型门的输入为x = 3,则门将计算输出f = 1.0 / (1.0 + Math.exp(-x)) = 0.95,然后其输入上的(局部)梯度将为dx = (0.95) * (1 - 0.95) = 0.0475。
这就是我们需要使用此门的全部内容:我们知道如何获取输入并通过S型门将其转发,并且还具有相对于其输入的渐变表达式,因此我们也可以通过它进行反向传播。还要注意的另一点是,从技术上讲,S型函数是由一行中的一系列门组成的,这些门计算更多的原子函数:幂门,加法门和除法门。这样处理就可以很好地工作,但是在这个示例中,我选择将所有这些门折叠成一个只用一枪就计算出S形的门,因为梯度表达式变得很简单。
让我们借此机会以一种很好的模块化方式仔细构造关联的代码。首先,我想请您注意,图中的每条线都有两个与之关联的数字:
它在向前传递过程中所携带的价值
在后退通道中流回的梯度(即拉力)
让我们创建一个简单的Unit结构,将这两个值存储在每条导线上。现在,我们的门将在Units上运行:它们将把它们作为输入并将其创建为输出。
// every Unit corresponds to a wire in the diagramsvar Unit = function(value, grad) {
// value computed in the forward pass
this.value = value;
// the derivative of circuit output w.r.t this unit, computed in backward pass
this.grad = grad; }除了单位我们还需要3门:+,*和sig(乙状结肠)。让我们从实现乘法门开始。我在这里使用Javascript,它具有一种通过函数模拟类的有趣方式。如果您不是Java脚本的熟悉者,那么这里要做的就是定义一个具有某些属性(使用this关键字访问)和一些方法(在Javascript中放入函数的原型中)的类。 。只需将它们视为类方法即可。还要记住,我们最终将使用这些方式的方法是,我们将首先forward一个接一个地打开所有门,然后backward以相反的顺序打开所有门。这是实现:
var multiplyGate = function(){ };multiplyGate.prototype = {
forward: function(u0, u1) {
// store pointers to input Units u0 and u1 and output unit utop
this.u0 = u0;
this.u1 = u1;
this.utop = new Unit(u0.value * u1.value, 0.0);
return this.utop;
},
backward: function() {
// take the gradient in output unit and chain it with the
// local gradients, which we derived for multiply gate before
// then write those gradients to those Units.
this.u0.grad += this.u1.value * this.utop.grad;
this.u1.grad += this.u0.value * this.utop.grad;
}}乘法门采用两个单位,每个单位都保存一个值,并创建一个存储其输出的单位。渐变被初始化为零。然后注意,在backward函数调用中,我们从前向传递过程中产生的输出单元中获取了渐变(现在希望可以填充其渐变),然后将其与该门的局部渐变相乘(链规则!)。该门u0.value * u1.value在正向传递过程中计算乘法(),因此请记住,梯度wrt u0为u1.value和wrt u1为u0.value。另外请注意,我们使用+=来添加到backward功能。这将使我们可能多次使用一个门的输出(将其视为分支的导线),因为事实证明,在计算相对于电路输出的最终梯度时,来自这些不同分支的梯度只是相加。其他两个门的定义类似:
var addGate = function(){ };addGate.prototype = {
forward: function(u0, u1) {
this.u0 = u0;
this.u1 = u1; // store pointers to input units
this.utop = new Unit(u0.value + u1.value, 0.0);
return this.utop;
},
backward: function() {
// add gate. derivative wrt both inputs is 1
this.u0.grad += 1 * this.utop.grad;
this.u1.grad += 1 * this.utop.grad;
}}var sigmoidGate = function() {
// helper function
this.sig = function(x) { return 1 / (1 + Math.exp(-x)); };};sigmoidGate.prototype = {
forward: function(u0) {
this.u0 = u0;
this.utop = new Unit(this.sig(this.u0.value), 0.0);
return this.utop;
},
backward: function() {
var s = this.sig(this.u0.value);
this.u0.grad += (s * (1 - s)) * this.utop.grad;
}}再次注意,backward在所有情况下,该函数仅针对其输入计算局部导数,然后乘以上方单位的斜率(即链法则)。为了完全指定所有内容,让我们最后用一些示例值写出二维神经元的前进和后退流程:
// create input unitsvar a = new Unit(1.0, 0.0);var b = new Unit(2.0, 0.0);var c = new Unit(-3.0, 0.0);var x = new Unit(-1.0, 0.0);var y = new Unit(3.0, 0.0);// create the gatesvar mulg0 = new multiplyGate();var mulg1 = new multiplyGate();var addg0 = new addGate();var addg1 = new addGate();var sg0 = new sigmoidGate();// do the forward passvar forwardNeuron = function() {
ax = mulg0.forward(a, x); // a*x = -1
by = mulg1.forward(b, y); // b*y = 6
axpby = addg0.forward(ax, by); // a*x + b*y = 5
axpbypc = addg1.forward(axpby, c); // a*x + b*y + c = 2
s = sg0.forward(axpbypc); // sig(a*x + b*y + c) = 0.8808};forwardNeuron();console.log('circuit output: ' + s.value); // prints 0.8808现在让我们计算梯度:只需以相反的顺序迭代并调用backward函数!请记住,在进行前向传递时我们存储了指向这些单元的指针,因此每个门都可以访问其输入以及先前生成的输出单元。
s.grad = 1.0;sg0.backward(); // writes gradient into axpbypcaddg1.backward(); // writes gradients into axpby and caddg0.backward(); // writes gradients into ax and bymulg1.backward(); // writes gradients into b and ymulg0.backward(); // writes gradients into a and x
请注意,第一行将输出(最后一个单位)1.0的渐变设置为从渐变链开始。这可以解释为以的力拉动最后一道闸门+1。换句话说,我们要拉动整个电路以产生会增加输出值的力。如果我们未将其设置为1,则由于链式规则中的乘法,所有梯度将被计算为零。最后,让输入响应计算的梯度并检查函数是否增加:
var step_size = 0.01;a.value += step_size * a.grad; // a.grad is -0.105b.value += step_size * b.grad; // b.grad is 0.315c.value += step_size * c.grad; // c.grad is 0.105x.value += step_size * x.grad; // x.grad is 0.105y.value += step_size * y.grad; // y.grad is 0.210forwardNeuron();console.log('circuit output after one backprop: ' + s.value); // prints 0.8825成功!0.8825高于先前的值0.8808。最后,让我们通过检查数字梯度来验证我们是否正确实现了反向传播:
var forwardCircuitFast = function(a,b,c,x,y) {
return 1/(1 + Math.exp( - (a*x + b*y + c))); };var a = 1, b = 2, c = -3, x = -1, y = 3;var h = 0.0001;var a_grad = (forwardCircuitFast(a+h,b,c,x,y) - forwardCircuitFast(a,b,c,x,y))/h;var b_grad = (forwardCircuitFast(a,b+h,c,x,y) - forwardCircuitFast(a,b,c,x,y))/h;var c_grad = (forwardCircuitFast(a,b,c+h,x,y) - forwardCircuitFast(a,b,c,x,y))/h;var x_grad = (forwardCircuitFast(a,b,c,x+h,y) - forwardCircuitFast(a,b,c,x,y))/h;var y_grad = (forwardCircuitFast(a,b,c,x,y+h) - forwardCircuitFast(a,b,c,x,y))/h;实际上,所有这些都提供与反向传播梯度相同的值[-0.105, 0.315, 0.105, 0.105, 0.210]。太好了!
我希望很明显,即使我们只看了单个神经元的示例,我上面给出的代码也以非常简单的方式进行了概括,以计算任意表达式(包括非常深的表达式#foreshadowing)的梯度。您所要做的就是编写小的门,计算输入的局部简单导数,将其连接到图形中,进行正向传递以计算输出值,然后进行反向传递以将梯度一直链接到输入。
成为反向道具忍者
随着时间的流逝,即使对于复杂的电路,也可以一次编写出反向遍历,效率将大大提高。让我们通过一些示例来练习反向传播。在下面的内容中,不必担心Unit,Circuit类,因为它们会混淆一些东西,而仅使用诸如的变量a,b,c,x,并da,db,dc,dx分别引用它们的渐变。同样,我们将变量视为每条导线的“正向流动”,将其梯度视为“反向流动”。我们的第一个例子是*大门:
var x = a * b;// and given gradient on x (dx), we saw that in backprop we would compute:var da = b * dx;var db = a * dx;
在上面的代码中,我假设dx给定了变量,它是在执行反向传播时从电路上方的某个位置来的(否则默认为+1)。之所以写出来,是因为我想明确显示渐变是如何链接在一起的。从等式中注意到,由于缺少更好的字,*门在反向传递期间充当切换器。它会记住其输入是什么,并且在前向传递期间,每个输入的梯度将成为另一个的值。然后,我们当然必须从上面乘以梯度,这就是链法则。这是+这种压缩形式的大门:
var x = a + b;// ->var da = 1.0 * dx;var db = 1.0 * dx;
1.0局部梯度在哪里,乘法是我们的链法则。加上三个数字呢?:
// lets compute x = a + b + c in two steps:var q = a + b; // gate 1var x = q + c; // gate 2// backward pass:dc = 1.0 * dx; // backprop gate 2dq = 1.0 * dx; da = 1.0 * dq; // backprop gate 1db = 1.0 * dq;
您可以看到发生了什么,对吧?如果您还记得向后流程图,则+闸门仅将梯度放在顶部并将其均等地路由到其所有输入(因为1.0对于所有输入,其局部梯度始终是简单的,而不管其实际值如何)。因此,我们可以更快地完成它:
var x = a + b + c;var da = 1.0 * dx; var db = 1.0 * dx; var dc = 1.0 * dx;
好吧,合并门如何?
var x = a * b + c;// given dx, backprop in-one-sweep would be =>da = b * dx;db = a * dx;dc = 1.0 * dx;
如果您看不到上面的情况,请引入一个临时变量q = a * b,然后进行计算x = q + c以说服自己。这是我们的神经元,让我们分两步进行:
// lets do our neuron in two steps:var q = a*x + b*y + c;var f = sig(q); // sig is the sigmoid function// and now backward pass, we are given df, and:var df = 1;var dq = (f * (1 - f)) * df;// and now we chain it to the inputsvar da = x * dq;var dx = a * dq;var dy = b * dq;var db = y * dq;var dc = 1.0 * dq;
我希望这开始变得更有道理。现在怎么样:
var x = a * a;var da = //???
您可以将其视为a流入门的值*,但导线会分开并成为两个输入。这实际上很简单,因为渐变的后向流总是加在一起。换句话说,什么都没有改变:
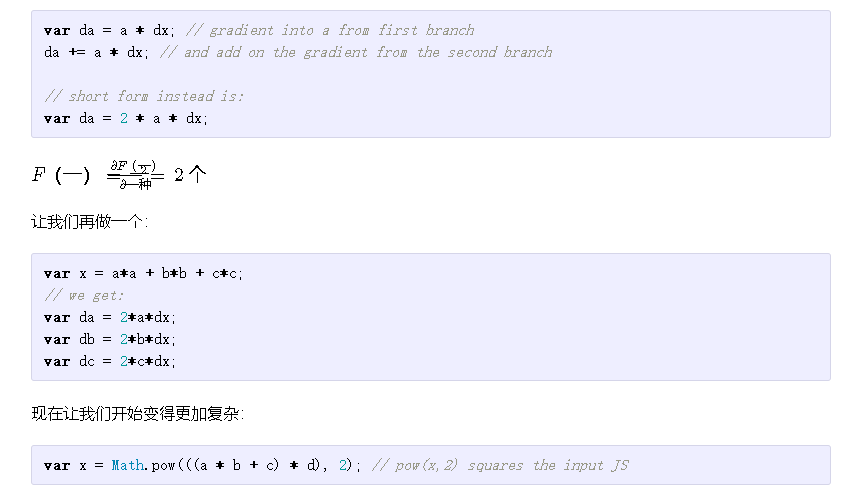
在实践中出现类似这种更复杂的情况时,我喜欢将表达式拆分为可管理的块,这些块几乎总是由更简单的表达式组成,然后将它们与链式规则链接在一起:
var x1 = a * b + c;var x2 = x1 * d;var x = x2 * x2; // this is identical to the above expression for x// and now in backprop we go backwards:var dx2 = 2 * x2 * dx; // backprop into x2var dd = x1 * dx2; // backprop into dvar dx1 = d * dx2; // backprop into x1var da = b * dx1;var db = a * dx1;var dc = 1.0 * dx1; // done!
那不是太困难!这些是整个表达式的反向支持方程式,我们将它们逐段完成,并反向支持所有变量。再次注意,对于正向传递过程中的每个变量,我们如何在反向传递过程中具有一个等效变量,其中包含相对于电路最终输出的梯度。以下是一些在实践中有用的有用函数及其局部梯度:
var x = 1.0/a; // divisionvar da = -1.0/(a*a);
实际中,这是划分的样子:
var x = (a + b)/(c + d);// lets decompose it in steps:var x1 = a + b;var x2 = c + d;var x3 = 1.0 / x2;var x = x1 * x3; // equivalent to above// and now backprop, again in reverse order:var dx1 = x3 * dx;var dx3 = x1 * dx;var dx2 = (-1.0/(x2*x2)) * dx3; // local gradient as shown above, and chain rulevar da = 1.0 * dx1; // and finally into the original variablesvar db = 1.0 * dx1;var dc = 1.0 * dx2;var dd = 1.0 * dx2;
希望您看到我们正在分解表达式,进行正向传递,然后对于每个变量(例如a),在我们da逐一返回时,应用简单的局部渐变并将它们与上面的渐变链接起来,以得出其渐变。这是另一个:
var x = Math.max(a, b);var da = a === x ? 1.0 * dx : 0.0;var db = b === x ? 1.0 * dx : 0.0;
好的,这使一件非常简单的事情难以阅读。该max函数传递最大的输入值,而忽略其他值。然后,在后向传递中,最大门将仅在顶部获得梯度并将其路由到在前向传递过程中实际流经它的输入。门控是一个简单的开关,基于该开关,在正向通过期间哪个输入的值最高。其他输入将具有零梯度。就是这样===,因为我们正在测试哪个输入是实际的最大值,并且仅将梯度传递给它。
最后,让我们看一下您可能听说过的整流线性单位非线性(或ReLU)。它在神经网络中代替了S型函数。它只是将阈值设为零:
var x = Math.max(a, 0)// backprop through this gate will then be:var da = a > 0 ? 1.0 * dx : 0.0;
换句话说,此门仅在值大于0时才传递该值,否则它将停止流并将其设置为零。在后向传递中,如果门在前次传递中被激活,则将从顶部通过梯度,或者如果原始输入小于零,则它将停止梯度流动。
我将在这一点上停止。我希望您对如何计算整个表达式(沿途由许多门组成)以及如何为每个表达式计算反向传递性有一些直觉。
我们在本章所做的一切都归结为:我们看到我们可以通过任意复杂的实值电路提供一些输入,在电路的末端以一定的力进行拖曳,然后反向传播将该拖曳分布到整个电路中。返回输入的方式。如果输入沿拖船的最终方向略有响应,则电路将沿原始拉动方向“略微”下降。也许这不是很明显,但是这个机器是一个强大的锤子机器学习。
“也许这不是很明显,但是这个机器是一个强大的锤子机器学习。”
现在让我们充分利用这台机器。
第2章:机器学习
在上一章中,我们关注的是实值电路,这些电路计算了输入的可能复杂表达式(前向通过),并且还可以计算原始输入(后向传递)上这些表达式的梯度。在本章中,我们将看到这种极其简单的机制在机器学习中的有用性。
二进制分类
和以前一样,让我们从简单开始。机器学习中最简单,常见但非常实用的问题是二进制分类。许多非常有趣和重要的问题都可以解决。设置如下:我们得到了一个N向量数据集,每个向量都用a +1或a 标记-1。例如,在二维中,我们的数据集可能看起来很简单:
vector -> label---------------[1.2, 0.7] -> +1[-0.3, 0.5] -> -1[-3, -1] -> +1[0.1, 1.0] -> -1[3.0, 1.1] -> -1[2.1, -3] -> +1
在这里,我们有N = 6 数据点,其中每个数据点都有两个功能(D = 2)。其中三个数据点带有标签 +1,另外三个标签-1。这是一个愚蠢的玩具示例,但实际上+ 1 / -1数据集可能确实是非常有用的东西:例如垃圾邮件/无垃圾邮件电子邮件,其中的载体以某种方式测量电子邮件内容的各种特征,例如数字有时提到某些增强药物。
目标。我们进行二进制分类的目标是学习一个采用二维向量并预测标签的函数。该函数通常由一组特定的参数来参数化,我们将需要调整该函数的参数,以使其输出与提供的数据集中的标签一致。最后,我们可以丢弃数据集,并使用学习到的参数来预测以前看不见的向量的标签。
训练规程
我们最终将构建完整的神经网络和复杂的表达式,但让我们从简单开始,并训练与我们在第1章末尾看到的单个神经元非常相似的线性分类器。唯一的区别是,我们将摆脱乙状结肠,因为它使事情变得不必要地复杂(我在第一章中仅以它为例,因为乙状结肠神经元在历史上很流行,但现代神经网络很少使用乙状结肠非线性)。无论如何,让我们使用一个简单的线性函数:
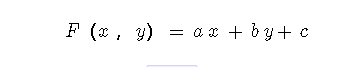
在此表达式中,我们将x其y视为输入(2D向量)以及a,b,c将要学习的函数的参数。例如,如果a = 1, b = -2, c = -1,则该函数将采用第一个数据点([1.2, 0.7])并输出1 * 1.2 + (-2) * 0.7 + (-1) = -1.2。这是培训的工作方式:
我们选择一个随机数据点,并将其通过电路
我们将把电路的输出解释为数据点具有类的置信度
+1。(即,非常高的值=电路确定该数据点具有等级,+1而非常低的值=电路确定该数据点具有等级-1。)我们将测量预测与提供的标签的匹配程度。直观地讲,例如,如果一个正例的得分非常低,我们将希望在电路的正方向上进行拉拔,要求它为此数据点输出更高的值。请注意,第一个数据点就是这种情况:它被标记为,
+1但我们的预测函数仅为其分配value-1.2。因此,我们将沿正方向拉动电路;我们希望价值更高。电路将采用拖船并反向传播以计算输入端的拖船
a,b,c,x,y由于我们将其
x,y视为(固定)数据点,因此我们将忽略pull onx,y。如果您是我的物理类比的爱好者,可以将这些输入视为固定在地面上的钉子。另一方面,我们将获取参数
a,b,c并使其对拖船做出响应(即,我们将执行所谓的参数更新)。当然,这样做可以使电路将来在该特定数据点上输出更高的分数。重复!返回步骤1。
我上面描述的训练方案通常称为随机梯度下降。我想重申的一个有趣的部分是,a,b,c,x,y就电路而言,它们全部由相同的内容组成:它们是电路的输入,电路将沿某个方向拉动它们。它不知道参数和数据点之间的区别。但是,在完成向后传递之后,我们将忽略数据点(x,y)上的所有拖轮,并在迭代数据集中的示例时继续将它们拖入和拔出。另一方面,我们保留参数(a,b,c),并在每次采样数据点时继续对其进行处理。随着时间的流逝,对这些参数的拉动将以某种方式调整这些值,以使该函数对正例输出高分,对负例输出低分。
学习支持向量机
支持向量机“强制规范”:
如果我们通过SVM电路馈入正数据点,并且输出值小于1,则用力拉动电路
+1。这是一个积极的例子,因此我们希望得分更高。相反,如果我们通过SVM提供一个负数据点并且输出大于-1,则电路为该数据点提供了危险的高分:用力向下拉电路
-1。除了上面的拉取之外,请始终在参数上添加少量拉取
a,b(注意,不要对c!进行拉取),以将其拉向零。您可以将两者都a,b视为附加到零附加的物理弹簧上。就像物理弹簧一样,这将使拉力与每种值a,b(物理学上的胡克定律,有人吗?)成正比。例如,如果a变得非常高,它将经历一个强烈的幅度|a|拉回零。这是拉我们所说的东西合法化,并可以确保无论我们的参数a或者b得到不成比例的大。这将是不希望的,因为两者a,b都会乘以输入要素x,y(请记住,等式为a*x + b*y + c),因此如果它们中的任何一个过高,我们的分类器都会对这些功能过于敏感。这不是一个很好的属性,因为在实践中功能通常很嘈杂,因此我们希望分类器摆动时相对平稳地进行更改。
让我们快速通过一个小而具体的例子。假设我们从一个随机参数设置开始,例如a = 1, b = -2, c = -1。然后:
如果我们提供分数
[1.2, 0.7],SVM将计算分数1 * 1.2 + (-2) * 0.7 - 1 = -1.2。该点+1在训练数据中被标记为,因此我们希望分数高于1。因此,电路顶部的坡度将为正:+1,它将反向传播至a,b,c。此外,还将有一个正则化拉a大-1(使其更小)和正则化拉b大+2其使其朝零的方向。假设我们将数据点馈送
[-0.3, 0.5]到SVM。它计算1 * (-0.3) + (-2) * 0.5 - 1 = -2.3。此点的标签为-1,并且由于-2.3小于-1,我们看到根据我们的力规格,SVM应该很高兴:计算得出的分数非常负,与本示例的负标签一致。由于不需要进行任何更改,因此电路的末尾将没有拉力(即为零)。然而,将仍然是对正规化拉a的-1和对b的+2。
好的,文本太多了。让我们编写SVM代码并利用我们在第1章中获得的电路机制:
// A circuit: it takes 5 Units (x,y,a,b,c) and outputs a single Unit// It can also compute the gradient w.r.t. its inputsvar Circuit = function() {
// create some gates
this.mulg0 = new multiplyGate();
this.mulg1 = new multiplyGate();
this.addg0 = new addGate();
this.addg1 = new addGate();};Circuit.prototype = {
forward: function(x,y,a,b,c) {
this.ax = this.mulg0.forward(a, x); // a*x
this.by = this.mulg1.forward(b, y); // b*y
this.axpby = this.addg0.forward(this.ax, this.by); // a*x + b*y
this.axpbypc = this.addg1.forward(this.axpby, c); // a*x + b*y + c
return this.axpbypc;
},
backward: function(gradient_top) { // takes pull from above
this.axpbypc.grad = gradient_top;
this.addg1.backward(); // sets gradient in axpby and c
this.addg0.backward(); // sets gradient in ax and by
this.mulg1.backward(); // sets gradient in b and y
this.mulg0.backward(); // sets gradient in a and x
}}那是只计算a*x + b*y + c并且也可以计算梯度的电路。它使用了我们在第1章中开发的Gates代码。现在让我们编写SVM,它并不关心实际电路。它只关心从中得出的值,并拉动电路。
// SVM classvar SVM = function() {
// random initial parameter values
this.a = new Unit(1.0, 0.0);
this.b = new Unit(-2.0, 0.0);
this.c = new Unit(-1.0, 0.0);
this.circuit = new Circuit();};SVM.prototype = {
forward: function(x, y) { // assume x and y are Units
this.unit_out = this.circuit.forward(x, y, this.a, this.b, this.c);
return this.unit_out;
},
backward: function(label) { // label is +1 or -1
// reset pulls on a,b,c
this.a.grad = 0.0;
this.b.grad = 0.0;
this.c.grad = 0.0;
// compute the pull based on what the circuit output was
var pull = 0.0;
if(label === 1 && this.unit_out.value < 1) {
pull = 1; // the score was too low: pull up
}
if(label === -1 && this.unit_out.value > -1) {
pull = -1; // the score was too high for a positive example, pull down
}
this.circuit.backward(pull); // writes gradient into x,y,a,b,c
// add regularization pull for parameters: towards zero and proportional to value
this.a.grad += -this.a.value;
this.b.grad += -this.b.value;
},
learnFrom: function(x, y, label) {
this.forward(x, y); // forward pass (set .value in all Units)
this.backward(label); // backward pass (set .grad in all Units)
this.parameterUpdate(); // parameters respond to tug
},
parameterUpdate: function() {
var step_size = 0.01;
this.a.value += step_size * this.a.grad;
this.b.value += step_size * this.b.grad;
this.c.value += step_size * this.c.grad;
}};现在让我们用随机梯度下降训练SVM:
var data = []; var labels = [];data.push([1.2, 0.7]); labels.push(1);data.push([-0.3, -0.5]); labels.push(-1);data.push([3.0, 0.1]); labels.push(1);data.push([-0.1, -1.0]); labels.push(-1);data.push([-1.0, 1.1]); labels.push(-1);data.push([2.1, -3]); labels.push(1);var svm = new SVM();// a function that computes the classification accuracyvar evalTrainingAccuracy = function() {
var num_correct = 0;
for(var i = 0; i < data.length; i++) {
var x = new Unit(data[i][0], 0.0);
var y = new Unit(data[i][1], 0.0);
var true_label = labels[i];
// see if the prediction matches the provided label
var predicted_label = svm.forward(x, y).value > 0 ? 1 : -1;
if(predicted_label === true_label) {
num_correct++;
}
}
return num_correct / data.length;};// the learning loopfor(var iter = 0; iter < 400; iter++) {
// pick a random data point
var i = Math.floor(Math.random() * data.length);
var x = new Unit(data[i][0], 0.0);
var y = new Unit(data[i][1], 0.0);
var label = labels[i];
svm.learnFrom(x, y, label);
if(iter % 25 == 0) { // every 10 iterations...
console.log('training accuracy at iter ' + iter + ': ' + evalTrainingAccuracy());
}}此代码输出以下输出:
training accuracy at iteration 0: 0.3333333333333333training accuracy at iteration 25: 0.3333333333333333training accuracy at iteration 50: 0.5training accuracy at iteration 75: 0.5training accuracy at iteration 100: 0.3333333333333333training accuracy at iteration 125: 0.5training accuracy at iteration 150: 0.5training accuracy at iteration 175: 0.5training accuracy at iteration 200: 0.5training accuracy at iteration 225: 0.6666666666666666training accuracy at iteration 250: 0.6666666666666666training accuracy at iteration 275: 0.8333333333333334training accuracy at iteration 300: 1training accuracy at iteration 325: 1training accuracy at iteration 350: 1training accuracy at iteration 375: 1
我们看到,最初我们的分类器仅具有33%的训练准确度,但最终所有训练示例都是正确的分类器,因为参数a,b,c根据我们施加的拉力调整了它们的值。我们刚刚培训了一个SVM!但是请不要在生产中的任何地方使用此代码:)一旦了解了核心内容,我们将看到如何使事情变得更加高效。
所需的迭代次数。在此示例数据,此示例初始化以及我们使用的步长设置的情况下,花了大约300次迭代来训练SVM。实际上,根据问题的严重性,初始化方式,数据规范化程度,使用的步长大小等因素,这个数目可能更多或更少。这只是一个玩具演示,但稍后我们将介绍所有最佳实践,以实际训练这些分类器。例如,事实证明,步长的设置非常重要和棘手。小步长会使模型训练缓慢。较大的步长将训练得更快,但是如果步长太大,则会使您的分类器混乱地跳动,而无法收敛到好的最终结果。
我想让您欣赏的一件事是,电路可以是任意表达式,而不仅仅是我们在本示例中使用的线性预测函数。例如,它可以是整个神经网络。
顺便说一句,我有意以模块化的方式构造代码,但是我们可以用更简单的代码来训练SVM。所有这些类和计算实际上可以归结为以下内容:
var a = 1, b = -2, c = -1; // initial parametersfor(var iter = 0; iter < 400; iter++) {
// pick a random data point
var i = Math.floor(Math.random() * data.length);
var x = data[i][0];
var y = data[i][1];
var label = labels[i];
// compute pull
var score = a*x + b*y + c;
var pull = 0.0;
if(label === 1 && score < 1) pull = 1;
if(label === -1 && score > -1) pull = -1;
// compute gradient and update parameters
var step_size = 0.01;
a += step_size * (x * pull - a); // -a is from the regularization
b += step_size * (y * pull - b); // -b is from the regularization
c += step_size * (1 * pull);}该代码给出了相同的结果。也许现在您可以看一下代码,看看这些方程式是如何产生的。
可变拉力?此时,请注意以下几点:您可能已经注意到,拉力始终为1,0或-1。您可以想象做其他事情,例如使此拉动与错误的严重程度成正比。这导致了SVM的变化,有人将其称为平方铰链损耗 SVM,其原因稍后将变得清楚。根据数据集的各种功能,可能会更好或更坏。例如,如果您的数据中有非常差的异常值,例如获得分数的负数据点+100,则其对我们分类器的影响将相对较小,因为-1无论错误有多严重,我们都将用力拉。实际上,我们将分类器的此属性称为对异常值的鲁棒性。
让我们回顾一下。我们介绍了二进制分类问题,其中给了我们N个D维向量,每个向量都有一个标签+ 1 / -1。我们看到我们可以将这些功能与实值电路(例如本例中的支持向量机电路)中的一组参数结合起来。然后,我们可以重复地通过电路传递数据,并每次调整参数,以使电路的输出值与所提供的标签一致。调整至关重要地取决于我们在电路中反向传播梯度的能力。最后,最终电路可用于预测未见实例的值!
将SVM推广到神经网络
令人感兴趣的是,一个SVM只是一个特定类型的非常简单的电路(电路计算score = a*x + b*y + c,其中a,b,c的权重和x,y为数据点)。这可以轻松扩展到更复杂的功能。例如,让我们编写一个进行二分类的2层神经网络。前向通行证将如下所示:
// assume inputs x,yvar n1 = Math.max(0, a1*x + b1*y + c1); // activation of 1st hidden neuronvar n2 = Math.max(0, a2*x + b2*y + c2); // 2nd neuronvar n3 = Math.max(0, a3*x + b3*y + c3); // 3rd neuronvar score = a4*n1 + b4*n2 + c4*n3 + d4; // the score
上面的规范是一个2层神经网络,具有3个隐藏的神经元(n1,n2,n3),在每个隐藏的神经元上使用整流线性单位(ReLU)非线性。如您所见,现在涉及多个参数,这意味着我们的分类器比简单的线性决策规则(例如SVM)更复杂,并且可以表示更复杂的决策边界。另一种思考的方式是,三个隐藏的神经元中的每个神经元都是线性分类器,现在我们在此之上放置一个额外的线性分类器。现在我们开始更深入 :)。好吧,让我们训练这个2层神经网络。该代码看起来与上面的SVM示例代码非常相似,我们只需要更改前向通过和后向通过:
// random initial parametersvar a1 = Math.random() - 0.5; // a random number between -0.5 and 0.5// ... similarly initialize all other parameters to randomsfor(var iter = 0; iter < 400; iter++) {
// pick a random data point
var i = Math.floor(Math.random() * data.length);
var x = data[i][0];
var y = data[i][1];
var label = labels[i];
// compute forward pass
var n1 = Math.max(0, a1*x + b1*y + c1); // activation of 1st hidden neuron
var n2 = Math.max(0, a2*x + b2*y + c2); // 2nd neuron
var n3 = Math.max(0, a3*x + b3*y + c3); // 3rd neuron
var score = a4*n1 + b4*n2 + c4*n3 + d4; // the score
// compute the pull on top
var pull = 0.0;
if(label === 1 && score < 1) pull = 1; // we want higher output! Pull up.
if(label === -1 && score > -1) pull = -1; // we want lower output! Pull down.
// now compute backward pass to all parameters of the model
// backprop through the last "score" neuron
var dscore = pull;
var da4 = n1 * dscore;
var dn1 = a4 * dscore;
var db4 = n2 * dscore;
var dn2 = b4 * dscore;
var dc4 = n3 * dscore;
var dn3 = c4 * dscore;
var dd4 = 1.0 * dscore; // phew
// backprop the ReLU non-linearities, in place
// i.e. just set gradients to zero if the neurons did not "fire"
var dn3 = n3 === 0 ? 0 : dn3;
var dn2 = n2 === 0 ? 0 : dn2;
var dn1 = n1 === 0 ? 0 : dn1;
// backprop to parameters of neuron 1
var da1 = x * dn1;
var db1 = y * dn1;
var dc1 = 1.0 * dn1;
// backprop to parameters of neuron 2
var da2 = x * dn2;
var db2 = y * dn2;
var dc2 = 1.0 * dn2;
// backprop to parameters of neuron 3
var da3 = x * dn3;
var db3 = y * dn3;
var dc3 = 1.0 * dn3;
// phew! End of backprop!
// note we could have also backpropped into x,y
// but we do not need these gradients. We only use the gradients
// on our parameters in the parameter update, and we discard x,y
// add the pulls from the regularization, tugging all multiplicative
// parameters (i.e. not the biases) downward, proportional to their value
da1 += -a1; da2 += -a2; da3 += -a3;
db1 += -b1; db2 += -b2; db3 += -b3;
da4 += -a4; db4 += -b4; dc4 += -c4;
// finally, do the parameter update
var step_size = 0.01;
a1 += step_size * da1;
b1 += step_size * db1;
c1 += step_size * dc1;
a2 += step_size * da2;
b2 += step_size * db2;
c2 += step_size * dc2;
a3 += step_size * da3;
b3 += step_size * db3;
c3 += step_size * dc3;
a4 += step_size * da4;
b4 += step_size * db4;
c4 += step_size * dc4;
d4 += step_size * dd4;
// wow this is tedious, please use for loops in prod.
// we're done!}这就是您训练神经网络的方式。显然,您希望很好地模块化您的代码,但是我为您扩展了此示例,希望它使事情变得更加具体和易于理解。稍后,我们将研究实现这些网络时的最佳实践,并且我们将以模块化,更明智的方式更整洁地构建代码。
但就目前而言,我希望您能获得一个收获,那就是2层神经网络确实不是一件令人恐惧的事情:我们编写一个前向通过表达式,将最后的值解释为分数,然后将其取值到正方向或负方向,具体取决于我们希望当前示例中的值是什么。反向传播后的参数更新将确保在将来看到此特定示例时,网络将更有可能给我们提供我们想要的值,而不是它在更新前给出的值。
更为传统的方法:损失函数
现在,我们了解了这些电路如何与数据一起工作的基础知识,让我们采用一种更常规的方法,您可能会在互联网上的其他地方以及其他教程和书籍中看到这种方法。您不会看到人们过多谈论力的规格。取而代之的是根据损失函数(或成本函数或目标)指定机器学习算法。
当我发展这种形式主义时,我也想对我们如何命名变量和参数开始更加谨慎。我希望这些方程看起来与您在书或其他教程中可能看到的相似,所以让我使用更多的标准命名约定。
示例:二维支持向量机
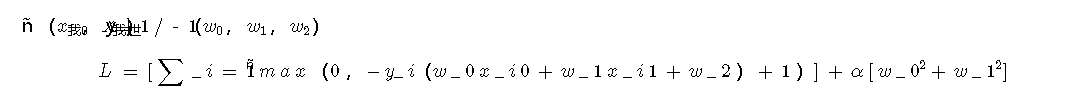
注意,由于第一个表达式中的阈值为零且正则化为平方,因此该表达式始终为正。想法是我们希望该表达式尽可能小。在深入探讨其细微差别之前,让我先将其翻译为代码:
var X = [ [1.2, 0.7], [-0.3, 0.5], [3, 2.5] ] // array of 2-dimensional datavar y = [1, -1, 1] // array of labelsvar w = [0.1, 0.2, 0.3] // example: random numbersvar alpha = 0.1; // regularization strengthfunction cost(X, y, w) {
var total_cost = 0.0; // L, in SVM loss function above
N = X.length;
for(var i=0;i<N;i++) {
// loop over all data points and compute their score
var xi = X[i];
var score = w[0] * xi[0] + w[1] * xi[1] + w[2];
// accumulate cost based on how compatible the score is with the label
var yi = y[i]; // label
var costi = Math.max(0, - yi * score + 1);
console.log('example ' + i + ': xi = (' + xi + ') and label = ' + yi);
console.log(' score computed to be ' + score.toFixed(3));
console.log(' => cost computed to be ' + costi.toFixed(3));
total_cost += costi;
}
// regularization cost: we want small weights
reg_cost = alpha * (w[0]*w[0] + w[1]*w[1])
console.log('regularization cost for current model is ' + reg_cost.toFixed(3));
total_cost += reg_cost;
console.log('total cost is ' + total_cost.toFixed(3));
return total_cost;}这是输出:
cost for example 0 is 0.440cost for example 1 is 1.370cost for example 2 is 0.000regularization cost for current model is 0.005total cost is 1.815
注意这个表达式是如何工作的:它的措施如何坏我们的SVM分类。让我们明确地执行以下操作:
xi = [1.2, 0.7]带标签的第一个数据yi = 1点将给出得分0.1*1.2 + 0.2*0.7 + 0.3,即0.56。请注意,这是一个积极的例子,因此我们希望得分大于+1。0.56是不足够的。实际上,此数据点的成本表达式将计算为costi = Math.max(0, -1*0.56 + 1),即0.44。您可以将成本视为量化SVM的不满。xi = [-0.3, 0.5]带有标签的第二个数据yi = -1点将给出得分0.1*(-0.3) + 0.2*0.5 + 0.3,即0.37。这看起来不太好:对于一个负面的例子,这个分数很高。它应该小于-1。确实,当我们计算成本:时costi = Math.max(0, 1*0.37 + 1),我们得到1.37。从这个例子中,这是非常高的成本,因为它被错误分类。最后一个
xi = [3, 2.5]带有label的示例yi = 1给出了score0.1*3 + 0.2*2.5 + 0.3,即1.1。在这种情况下,SVM将计算costi = Math.max(0, -1*1.1 + 1),实际上为零。该数据点已正确分类,并且没有与此相关的成本。
成本函数是一个度量,用来衡量分类器的不良程度。当训练集被完美分类时,成本(忽略正则化)将为零。
请注意,损失中的最后一项是正则化成本,这表示我们的模型参数应为较小的值。由于这个术语,成本实际上将永远不会为零(因为这将意味着除偏差以外的所有模型参数都完全为零),但是我们越接近,分类器就越好。
机器学习中的大多数成本函数由两部分组成:1.一部分用于衡量模型对数据的拟合程度,以及2:正则化,用于衡量模型的复杂程度或可能性。
我希望我能说服您,要获得一个很好的SVM,我们真的想使成本尽可能小。听起来很熟悉?我们确切地知道该怎么做:上面写的成本函数是我们的电路。我们将通过电路转发所有的例子,计算后向通行,并更新所有参数,使得电路将输出一个较小的未来成本。具体来说,我们将计算梯度,然后在与梯度相反的方向上更新参数(因为我们希望使成本变小而不是变大)。
“我们确切地知道该怎么做:上面写的成本函数是我们的电路。”
待办事项:清理本节并将其充实一下……
第三章:实践中的反向传播
建立图书馆
示例:实用神经网络分类器
多类:结构化SVM
多类:Logistic回归,Softmax
示例:回归
成本函数需要微小的变化。L2正则化。
示例:结构化预测
基本思想是训练(非规范化)能量模型
向量化的实现
用numpy在Python中编写神经网络类。
反向传播实践:技巧/窍门
成本功能监控
监控培训/验证绩效
调整初始学习率,学习率时间表
优化:使用动量
优化:LBFGS,Nesterov加速梯度
初始化的重要性:权重和偏差
正则化:L2,L1,组稀疏性,辍学
超参数搜索,交叉验证
常见陷阱:(例如垂死的ReLU)
处理不平衡的数据集
无法正常工作时调试网络的方法
第4章:野外网络
在实践中运行良好且已在野外部署的模型的案例研究。
案例研究:图像的卷积神经网络
卷积层,池化,AlexNet等
案例研究:语音和文本的递归神经网络
香草循环网,双向循环网。也许LSTM概述
案例研究:Word2Vec
在NLP中训练单词向量表示
案例研究:t-SNE
训练嵌入以可视化数据
致谢
非常感谢以下使本指南变得更好的人:wodenokoto(HN),zackmorris(HN)。
评论
本指南尚在开发中,我非常感谢您提供反馈,尤其是对于不清楚或仅能理解的部分。谢谢!
本教程中的一些Javascript代码已由Ajit转换为Python,可以在Github上找到它。


评论专区