Q-Learning By Examples

Q-Learning By Examples

In this tutorial, you will discover step by step how an agent learns through training without teacher (unsupervised) in unknown environment. You will find out part of reinforcement learning algorithm called Q-learning. Reinforcement learning algorithm has been widely used for many applications such as robotics, multi agent system, game, and etc.

Instead of learning the theory of reinforcement that you can read it from many books and other web sites (see Resources for more references), in this tutorial will introduce the concept through simple but comprehensive numerical example. You may also download the Matlab code or MS Excel Spreadsheet for free.

Suppose we have 5 rooms in a building connected by certain doors as shown in the figure below. We give name to each room A to E. We can consider outside of the building as one big room to cover the building, and name it as F. Notice that there are two doors lead to the building from F, that is through room B and room E.

We can represent the rooms by graph, each room as a vertex (or node) and each door as an edge (or link). Refer to my other tutorial on Graph if you are not sure about what is Graph.
 

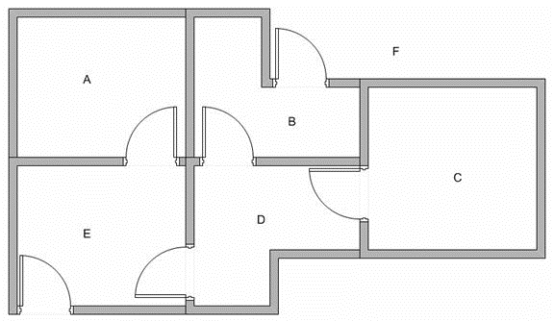
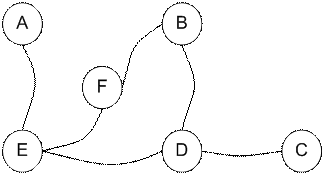
We want to set the target room. If we put an agent in any room, we want the agent to go outside the building. In other word, the goal room is the node F. To set this kind of goal, we introduce give a kind of reward value to each door (i.e. edge of the graph). The doors that lead immediately to the goal have instant reward of 100 (see diagram below, they have red arrows). Other doors that do not have direct connection to the target room have zero reward. Because the door is two way (from A can go to E and from E can go back to A), we assign two arrows to each room of the previous graph. Each arrow contains an instant reward value. The graph becomes state diagram as shown below

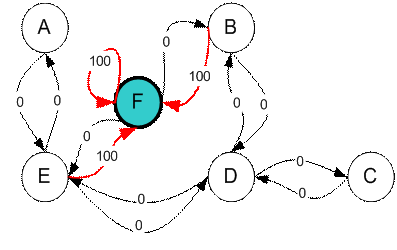
Additional loop with highest reward (100) is given to the goal room (F back to F) so that if the agent arrives at the goal, it will remain there forever. This type of goal is called absorbing goal because when it reaches the goal state, it will stay in the goal state.

Ladies and gentlemen, now is the time to introduce our superstar agent….

Imagine our agent as a dumb virtual robot that can learn through experience. The agent can pass one room to another but has no knowledge of the environment. It does not know which sequence of doors the agent must pass to go outside the building.

Suppose we want to model some kind of simple evacuation of an agent from any room in the building. Now suppose we have an agent in Room C and we want the agent to learn to reach outside the house (F). (see diagram below)
 

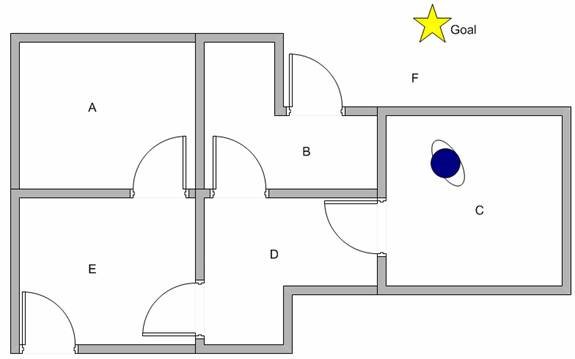
How to make our agent learn from experience?

Before we discuss about how the agent will learn (using Q learning) in the next section, let us discuss about some terminologies of state and action .

We call each room (including outside the building) as a state . Agent's movement from one room to another room is called action . Let us draw back our state diagram. State is depicted using node in the state diagram, while action is represented by the arrow.

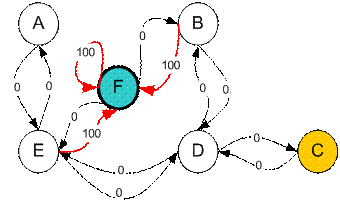
Suppose now the agent is in state C. From state C, the agent can go to state D because the state C is connected to D. From state C, however, the agent cannot directly go to state B because there is no direct door connecting room B and C (thus, no arrow). From state D, the agent can go either to state B or state E or back to state C (look at the arrow out of state D). If the agent is in state E, then three possible actions are to go to state A, or state F or state D. If agent is state B, it can go either to state F or state D. From state A, it can only go back to state E.

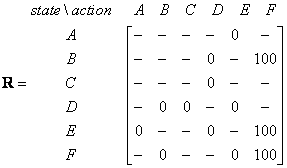
We can put the state diagram and the instant reward values into the following reward table, or matrix R .

	Action to go to state
Agent now in state	A	B	C	D	E	F
A	-	-	-	-	0	-
B	-	-	-	0	-	100
C	-	-	-	0	-	-
D	-	0	0	-	0	-
E	0	-	-	0	-	100
F	-	0	-	-	0	100

The minus sign in the table says that the row state has no action to go to column state. For example, State A cannot go to state B (because no door connecting room A and B, remember?)

In the previous sections of this tutorial, we have modeled the environment and the reward system for our agent. This section will describe learning algorithm called Q learning (which is a simplification of reinforcement learning).

We have model the environment reward system as matrix R.

Now we need to put similar matrix name Q in the brain of our agent that will represent the memory of what the agent have learned through many experiences. The row of matrix Q represents current state of the agent, the column of matrix Q pointing to the action to go to the next state.

In the beginning, we say that the agent know nothing, thus we put Q as zero matrix. In this example, for the simplicity of explanation, we assume the number of state is known (to be six). In more general case, you can start with zero matrix of single cell. It is a simple task to add more column and rows in Q matrix if a new state is found.

The transition rule of this Q learning is a very simple formula

The formula above have meaning that the entry value in matrix Q (that is row represent state and column represent action) is equal to corresponding entry of matrix R added by a multiplication of a learning parameter 

and maximum value of Q for all action in the next state.

Our virtual agent will learn through experience without teacher (this is called unsupervised learning). The agent will explore state to state until it reaches the goal. We call each exploration as an episode . In one episode the agent will move from initial state until the goal state. Once the agent arrives at the goal state, program goes to the next episode. The algorithm below has been proved to be convergence (See references for the proof)
 

Q Learning

Given : State diagram with a goal state (represented by matrix R)

Find : Minimum path from any initial state to the goal state (represented by matrix Q)

Q Learning Algorithm goes as follow Set parameter  , and environment reward matrix R Initialize matrix Q as zero matrix For each episode: Select one among all possible actions for the current state Using this possible action, consider to go to the next state Get maximum Q value of this next state based on all possible actions Compute  Set the next state as the current state Select random initial state Do while not reach goal state End Do End For

The above algorithm is used by the agent to learn from experience or training. Each episode is equivalent to one training session. In each training session, the agent explores the environment (represented by Matrix R ), get the reward (or none) until it reach the goal state. The purpose of the training is to enhance the ‘brain' of our agent that represented by Q matrix. More training will give better Q matrix that can be used by the agent to move in optimal way. In this case, if the Q matrix has been enhanced, instead of exploring around and go back and forth to the same room, the agent will find the fastest route to the goal state.

Parameter 

has range value of 0 to 1( 

). If 

is closer to zero, the agent will tend to consider only immediate reward. If 

is closer to one, the agent will consider future reward with greater weight, willing to delay the reward.

To use the Q matrix, the agent traces the sequence of states, from the initial state until goal state. The algorithm is as simple as finding action that makes maximum Q for current state:

Algorithm to utilize the Q matrix Input: Q matrix, initial state Set current state = initial state From current state, find action that produce maximum Q value Set current state = next state Go to 2 until current state = goal state

The algorithm above will return sequence of current state from initial state until goal state.

To understand how the Q learning algorithm works, we will go through several steps of numerical examples. The rest of the steps can be can be confirm using the program (you can freely download either MS Excel or Matlab code companion of this tutorial)
 

Let us set the value of learning parameter 

and initial state as room B.

First we set matrix Q as a zero matrix.

I put again the instant reward matrix R that represents the environment in here for your convenience.

Look at the second row (state B) of matrix R. There are two possible actions for the current state B, that is to go to state D, or go to state F. By random selection, we select to go to F as our action.

Now we consider that suppose we are in state F. Look at the sixth row of reward matrix R (i.e. state F). It has 3 possible actions to go to state B, E or F.

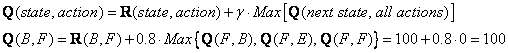
Since matrix Q that is still zero, 

are all zero. The result of computation 

is also 100 because of the instant reward.

The next state is F, now become the current state. Because F is the goal state, we finish one episode. Our agent's brain now contain updated matrix Q as

For the next episode, we start with initial random state. This time for instance we have state D as our initial state.

Look at the fourth row of matrix R; it has 3 possible actions, that is to go to state B, C and E. By random selection, we select to go to state B as our action.

Now we imagine that we are in state B. Look at the second row of reward matrix R (i.e. state B). It has 2 possible actions to go to state D or state F. Then, we compute the Q value

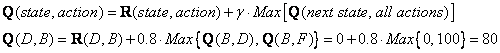
We use the updated matrix Q from the last episode. 

and 

. The result of computation 

because of the reward is zero. The Q matrix becomes

The next state is B, now become the current state. We repeat the inner loop in Q learning algorithm because state B is not the goal state.

For the new loop, the current state is state B. I copy again the state diagram that represent instant reward matrix R for your convenient.

There are two possible actions from the current state B, that is to go to state D, or go to state F. By lucky draw, our action selected is state F.

Now we think of state F that has 3 possible actions to go to state B, E or F. We compute the Q value using the maximum value of these possible actions.

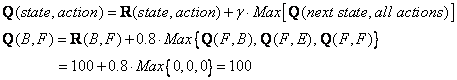
The entries of updated Q matrix contain 

are all zero. The result of computation 

is also 100 because of the instant reward. This result does not change the Q matrix.

Because F is the goal state, we finish this episode. Our agent's brain now contain updated matrix Q as

If our agent learns more and more experience through many episodes, it will finally reach convergence values of Q matrix as

This Q matrix, then can be normalized into a percentage by dividing all valid entries with the highest number (divided by 500 in this case) becomes

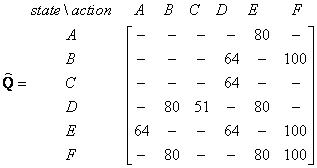
Once the Q matrix reaches almost the convergence value, our agent can reach the goal in an optimum way. To trace the sequence of states, it can easily compute by finding action that makes maximum Q for this state.

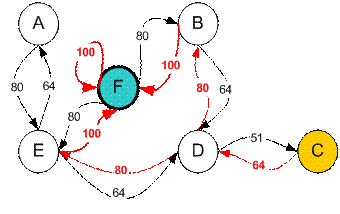
For example from initial State C, it can use the Q matrix as follow:

From State C the maximum Q produces action to go to state D

From State D the maximum Q has two alternatives to go to state B or E. Suppose we choose arbitrary to go to B

From State B the maximum value produces action to go to state F

Thus the sequence is C – D – B – F